Question

7．数轴是一个非常重要的数学工具，它使数和数轴上的点建立起对应关系，揭示了数与点之间的内在联系，它是“数形结合”的基础．小白在草稿纸上画了一条数轴进行操作探究：

操作一：
（1）折叠纸面，若使表示的点1与-1表示的点重合，则-2表示的点与2表示的点重合；
操作二：
（2）折叠纸面，若使1表示的点与-3表示的点重合，回答以下问题：
①$\sqrt{3}$表示的点与数-2-$\sqrt{3}$表示的点重合；
②若数轴上A、B两点之间距离为8（A在B的左侧），且A、B两点经折叠后重合，则A、B两点表示的数分别是-5和3；
操作三：
（3）在数轴上剪下9个单位长度（从-1到8）的一条线段，并把这条线段沿某点折叠，然后在重叠部分某处剪一刀得到三条线段（如图）．若这三条线段的长度之比为1：1：2，则折痕处对应的点所表示的数可能是$\frac{19}{8}$或$\frac{7}{2}$或$\frac{37}{8}$．

Answer 1

分析 （1）根据对称性找到折痕的点为原点O，可以得出-2与2重合；
（2）根据对称性找到折痕的点为-1，
①设$\sqrt{3}$表示的点与数a表示的点重合，根据对称性列式求出a的值；
②因为AB=8，所以A到折痕的点距离为4，因为折痕对应的点为-1，由此得出A、B两点表示的数；
（3）分三种情况进行讨论：设折痕处对应的点所表示的数是x，如图1，当AB：BC：CD=1：1：2时，所以设AB=a，BC=a，CD=2a，得a+a+2a=9，a=$\frac{9}{4}$，得出AB、BC、CD的值，计算也x的值，同理可得出如图2、3对应的x的值．

解答 解：操作一，
（1）∵表示的点1与-1表示的点重合，
∴折痕为原点O，
 则-2表示的点与2表示的点重合，
故答案为：2；
操作二：
（2）∵折叠纸面，若使1表示的点与-3表示的点重合，
则折痕表示的点为-1，
 ①设$\sqrt{3}$表示的点与数a表示的点重合，
则$\sqrt{3}$-（-1）=-1-a，
a=-2-$\sqrt{3}$；
②∵数轴上A、B两点之间距离为8，
∴数轴上A、B两点到折痕-1的距离为4，
∵A在B的左侧，
则A、B两点表示的数分别是-5和3；
故答案为：①-2-$\sqrt{3}$，②-5和3；
操作三：
（3）设折痕处对应的点所表示的数是x，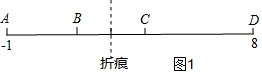
如图1，当AB：BC：CD=1：1：2时，
设AB=a，BC=a，CD=2a，
a+a+2a=9，
a=$\frac{9}{4}$，
∴AB=$\frac{9}{4}$，BC=$\frac{9}{4}$，CD=$\frac{9}{2}$，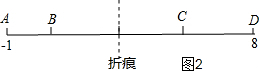
x=-1+$\frac{9}{4}$+$\frac{9}{8}$=$\frac{19}{8}$，
如图2，当AB：BC：CD=1：2：1时，
设AB=a，BC=2a，CD=a，
a+a+2a=9，
a=$\frac{9}{4}$，
∴AB=$\frac{9}{4}$，BC=$\frac{9}{2}$，CD=$\frac{9}{4}$，
x=-1+$\frac{9}{4}$+$\frac{9}{4}$=$\frac{7}{2}$，
如图3，当AB：BC：CD=2：1：1时，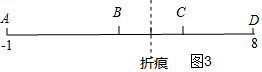
设AB=2a，BC=a，CD=a，
a+a+2a=9，
a=$\frac{9}{4}$，
∴AB=$\frac{9}{2}$，BC=CD=$\frac{9}{4}$，
x=-1+$\frac{9}{2}$+$\frac{9}{8}$=$\frac{37}{8}$，
综上所述：则折痕处对应的点所表示的数可能是$\frac{19}{8}$或$\frac{7}{2}$或$\frac{37}{8}$．
故答案为：$\frac{19}{8}$或$\frac{7}{2}$或$\frac{37}{8}$．

点评 本题考查了实数和数轴的关系，及数轴上的折叠变换问题，明确①数轴上折叠后重合的点到折痕的距离相等，②数轴上任意两点的距离为两点坐标的绝对值；本题第三问有难度，采用了分类讨论的思想．