
【题目】如图,在直角坐标系xoy中,已知A(6,0),B(8,6),将线段OA平移至CB,点D在x轴正半轴上(不与点A重合),连接OC,AB,CD,BD.
(1)写出点C的坐标;
(2)当△ODC的面积是△ABD的面积的3倍时,求点D的坐标;
(3)设∠OCD=α,∠DBA=β,∠BDC=θ,判断α、β、θ之间的数量关系,并说明理由.
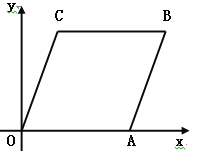
【答案】(1)点C的坐标为(2,6);
(2)点D的坐标是(![]() ,0)
,0)
(3)α﹣β=θ,理由见解析.
【解析】分析:(1)由点的坐标的特点,确定出FC=2,OF=6得出C(2,6) ;
(2)分点D在线段OA和在OA延长线两种情况进行计算;
(3)分点D在线段OA上时, ![]() 和在OA延长线
和在OA延长线![]() 两种情况进行计算;
两种情况进行计算;
解:(1)C(2,6);
(2)设D(x,0),当△ODC的面积是△ABD的面积的3倍时,
若点D在线段OA上,
∵OD=3AD,
∴![]() ×6x=3×
×6x=3×![]() ×6(6﹣x),
×6(6﹣x),
∴x=![]() ,
,
∴D(![]() ,0);
,0);
若点D在线段OA延长线上,
∵OD=3AD,
∴![]() ×6x=3×
×6x=3×![]() ×6(x﹣6),
×6(x﹣6),
∴x=9,
∴D(9,0)
(3)如图2.
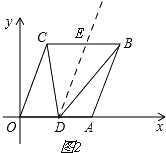
过点D作DE∥OC,
由平移的性质知OC∥AB.
∴OC∥AB∥DE.
∴∠OCD=∠CDE,∠EDB=∠DBA.
若点D在线段OA上,
∠CDB=∠CDE+∠EDB=∠OCD+∠DBA,
即α+β=θ;
若点D在线段OA延长线上,
∠CDB=∠CDE﹣∠EDB=∠OCD﹣∠DBA,
即α﹣β=θ.


 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:初中数学 来源: 题型:
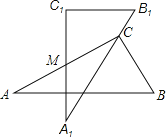
【题目】如图所示是两块完全一样的含30°角的三角板,分别记作△ABC和△A1B1C1,现将两块三角板重叠在一起,设较长直角边的中点为M,绕中点M转动三角板ABC,使其直角顶点C恰好落在三角板A1B1C1的斜边A1B1上,当∠A=30°,AC=10时,两直角顶点C,C1的距离是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的袋中装有5个黄球,13个黑球和22个红球,这些球除颜色外其他都相同.
(1)求从袋中摸出一个球是黄球的概率.
(2)现在从袋中取出若干个黑球,并放入相同数量的黄球,搅拌均匀后,使从袋中摸出一个球是黄球的概率不小于![]() ,问:至少取出多少个黑球?
,问:至少取出多少个黑球?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题中真命题是( )
A. 同旁内角相等,两直线平行
B. 两锐角之和为钝角
C. 到角的两边距离相等的点在这个角的平分线上
D. 直角三角形斜边上的中线等于斜边的一半
查看答案和解析>>
科目:初中数学 来源: 题型:
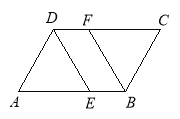
【题目】如图,四边形ABCD是平行四边形,DE平分∠ADC交AB于点E,BF平分∠ABC,交CD于点F.
(1)、求证:DE=BF;(2)、连接EF,写出图中所有的全等三角形.(不要求证明)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com