
【题目】如图(1)是一个长为 ![]() ,宽为
,宽为 ![]() (
( ![]() >
> ![]() )的长方形,用剪刀沿图中虚线(对称轴)剪开,把它分成四块形状和大小都一样的小长方形,然后按图(2)那样拼成一个正方形,则中间空的部分的面积是.
)的长方形,用剪刀沿图中虚线(对称轴)剪开,把它分成四块形状和大小都一样的小长方形,然后按图(2)那样拼成一个正方形,则中间空的部分的面积是.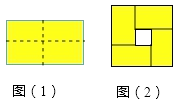
科目:初中数学 来源: 题型:
【题目】在面积为24的△ABC中,矩形DEFG的边DE在AB上运动,点F,G分别在边BC,AC上.
(1)若AB=8,DE=2EF,求GF的长;
(2)若![]() ,如图2,线段DM,EN分别为△ADG和△BEF的角平分线,求证:MG=NF;
,如图2,线段DM,EN分别为△ADG和△BEF的角平分线,求证:MG=NF;
(3)求出矩形DEFG的面积的最大值.
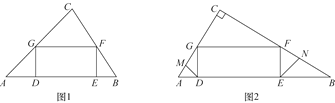
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抚州市正在争创省文明城市,为了美化城市,改善人们的居住环境,我市深入开展绿化彩化美化工程,通过植草、种树、修建公园及树阵式停车位等多项措施,使城区绿地面积不断增加.请根据图中所提供的信息,回答下列问题: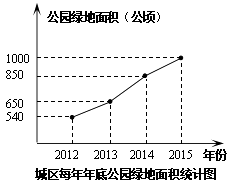
(1)2014年底的公园绿地面积为公顷,比2012年底增加了公顷;
(2)在2013年,2014年,2015年这三年中,绿地面积增加最多的是年;
(3)为满足城市发展的需要,计划到2017年底使城区公园绿地总面积达到1200公顷,试求2017年底公园绿地面积对2015年底的增长率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,设正方体ABCD-A1B1C1D1的棱长为1,黑、白两个甲壳虫同时从点A出发,以相同的速度分别沿棱向前爬行,黑甲壳虫爬行的路线是AA1→A1D1→……,白甲壳虫爬行的路线是AB→BB1→……,并且都遵循如下规则:所爬行的第n+2与第n条棱所在的直线必须是既不平行也不相交(其中n是正整数).那么当黑、白两个甲壳虫各爬行完第2015条棱分别停止在所到的正方体顶点处时,它们之间的距离是( ).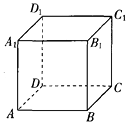
A.0 B.1 C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,对于点P(x , y)和Q(x , y′),给出如下定义:若 ![]() ,则称点Q为点P的“可控变点”.例如:点(1,2)的“可控变点”为点(1,2).
,则称点Q为点P的“可控变点”.例如:点(1,2)的“可控变点”为点(1,2).
结合定义,请回答下列问题: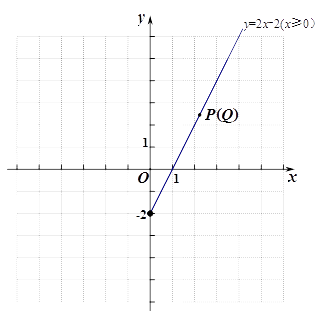
(1)点(-3,4)的“可控变点”为点 .
(2)若点N(m,2)是函数 ![]() 图象上点M的“可控变点”,则点M的坐标为;
图象上点M的“可控变点”,则点M的坐标为;
(3)点P为直线 ![]() 上的动点,当x≥0时,它的“可控变点”Q所形成的图象如下图所示(实线部分含实心点).请补全当x<0时,点P的“可控变点” Q所形成的图象;
上的动点,当x≥0时,它的“可控变点”Q所形成的图象如下图所示(实线部分含实心点).请补全当x<0时,点P的“可控变点” Q所形成的图象;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com