
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
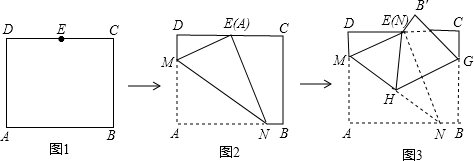
分析 根据折叠的性质可得EM∥GH,再根据等量代换,即可得出∠AMN=∠EHG;在直角三角形中运用勾股定理,即可得出AM=EM=7.4,再根据相似三角形的性质,即可得出EN=$\frac{37}{6}\sqrt{3}$=AN,进而得到tan∠AMN=$\frac{AN}{MN}$=$\frac{5}{6}\sqrt{3}$=tan∠EHG,最后根据∠EMH≠60°,可得△MEH不是等边三角形.
解答 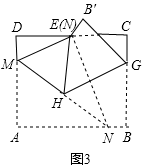 解:如图3,由折叠可得,∠MEN=∠A=90°,HG⊥NE,
解:如图3,由折叠可得,∠MEN=∠A=90°,HG⊥NE,
即ME⊥EN,HG⊥EN,
∴EM∥GH,故①正确;
∴∠NME=∠NHG,
由折叠可得,∠NME=∠AMN,∠EHG=∠NHG,
∴∠AMN=∠EHG,故③正确;
如图2,作NF⊥CD于F.
设DM=x,则AM=EM=10-x,
∵点E是CD的中点,AB=CD=8$\sqrt{3}$,
∴DE=$\frac{1}{2}$CD=4$\sqrt{3}$,
在Rt△DEM中,∵DM2+DE2=EM2,
∴(4$\sqrt{3}$)2+x2=(10-x)2,
解得x=2.6,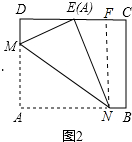
∴DM=2.6,AM=EM=7.4,
∵∠DEM+∠NEF=90°,∠NEF+∠ENF=90°,
∴∠DEM=∠ENF,
∵∠D=∠EFN=90°,
∴△DME∽△FEN,
∴$\frac{DE}{FN}$=$\frac{EM}{EN}$,即$\frac{4\sqrt{3}}{10}$=$\frac{7.4}{EN}$,
∴EN=$\frac{37}{6}\sqrt{3}$,
∴AN=$\frac{37}{6}\sqrt{3}$,
∴tan∠AMN=$\frac{AN}{MN}$=$\frac{5}{6}\sqrt{3}$,
∴tan∠EHG=$\frac{5\sqrt{3}}{6}$,故④正确;
又∵tan60°=$\sqrt{3}$>$\frac{5}{6}\sqrt{3}$,
∴∠AMN≠60°,即∠EMH≠60°,
∴△MEH不是等边三角形,故②错误.
∴正确的结论有3个.
故选:C.
点评 本题属于四边形综合题,主要考查翻折变换、勾股定理、相似三角形的判定和性质等知识的综合应用,解题的关键是作辅助线构造相似三角形,依据相似三角形对应边成比例,求得EN的长度.解决折叠问题时,常常设要求的线段长为x,然后根据折叠和轴对称的性质用含x的代数式表示其他线段的长度,选择适当的直角三角形,运用勾股定理列出方程求出答案.


科目:初中数学 来源: 题型:选择题
| A. | ① | B. | ② | C. | ③ | D. | ④ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0.612×107 | B. | 6.12×106 | C. | 61.2×105 | D. | 612×106 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 调查2017年2月份利辛市场上某品牌饮料的质量 | |
| B. | 调查某月份长江安徽段水域的水质量情况 | |
| C. | 光明节能厂检测一批新型节能灯的使用寿命 | |
| D. | 了解某班50名学生的年龄情况 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{x-2}{{x}^{2}-3x+2}$ | B. | $\frac{1}{x-2}$ | C. | $\frac{2x-4}{x-1}$ | D. | $\frac{x+2}{x+1}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com