
����Ŀ����֪�߶�![]() ��
�� ![]() ��
��![]() ��������ABC��ʹ
��������ABC��ʹ![]() ��
�� ![]() ��
�� ![]() ���ϵ�����
���ϵ�����![]() ������������˳������Ϊ�� ��
������������˳������Ϊ�� ��
���ӳ�![]() ��B��ʹ
��B��ʹ![]() ��������
��������![]() ��������ADC��ʹ
��������ADC��ʹ![]() ��
�� ![]() ��
�� ![]() ��
��
A. �ۢ٢� B. �٢ڢ� C. �ڢۢ� D. �ۢڢ�
���𰸡�A
�������������������������ADC�������ӳ������Ӽ��ɣ�
������֪�������ܹ�ȷ��������������ADC����������ADC��ʹDC=![]() a��AC=b��AD=m�����ӳ�CD��B��ʹBD=CD������AB�����ɵ���ABC��
a��AC=b��AD=m�����ӳ�CD��B��ʹBD=CD������AB�����ɵ���ABC��
�������ĺ���˳��Ϊ�ۢڢ�����ѡA��
���㣺���⿼����ǻ�����ͼ
�����������Ĺؼ�������������֪�����ε����ߺ�����һ���ϵ������������ε�������
�����͡���ѡ��
��������
6
����Ŀ����ͼ����ֱ�ߺ�Բ����һ���ǵ�����֪�ǵ�ʾ��ͼ����˵��![]() �������ǣ� ��
�������ǣ� ��


A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
 ���б�ˢ��ϵ�д�
���б�ˢ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������¼��У��DZ�Ȼ�¼����ǣ�������
A.�����˶�Ա����һ�Σ����������B.���ⷭ��һ���飬��ҳ��ҳ��������
C.�����н�ͨ�źŵƵ�·�ڣ������̵�D.���⻭һ�������Σ����ڽǺ���180��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��AE��CD�ཻ�ڵ�B������BFƽ�֡�ABC������BG�ڡ�ABD�ڣ�
��1������DBE�IJ�����������ǵ�3�������DBE�Ķ�����
��2���ڣ�1���ļ��£�����DBG=��ABG��33�������ABG�Ķ�����
��3������FBG=100�������ABG�͡�DBG�Ķ����IJ

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������OABC�����Ϊ9����OΪ����ԭ�㣬��B�ں���y= ![]() ��k��0��x��0����ͼ���ϵ�P��m��n���Ǻ���ͼ��������һ�㣬����P�ֱ���x��y��Ĵ��ߣ�����ֱ�ΪE��F���������OEPF��������OABC���غϵIJ��ֵ����ΪS��
��k��0��x��0����ͼ���ϵ�P��m��n���Ǻ���ͼ��������һ�㣬����P�ֱ���x��y��Ĵ��ߣ�����ֱ�ΪE��F���������OEPF��������OABC���غϵIJ��ֵ����ΪS�� 
��1����k��ֵ��
��2����S= ![]() ʱ����P������ꣻ
ʱ����P������ꣻ
��3��д��S����m�Ĺ�ϵʽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ����ϣ�
һ��أ���������Ϊ�����ʱ��tan����+�£���tan�������£���ֵ����������Ĺ�ʽ��ã�tan�������£�=![]() ��
��
���磺tan15��=tan��45�㩁30�㣩=![]() =
= =
=![]()
= =
=![]() ��
��
�������ϲ��ϣ�����������⣺
��1����tan75���ֵ��
��2�������ķ�����ԭ���ı�����ʼ��������������䣬ϵ���ľ�����ķ�����ľ�������٣�����������1983�꣬������������ά���ķ�������Ϊ������߲�����ʵ��ʯ����ͼ1����С��������ѧ֪ʶ������������ĸ߶ȣ���ͼ2����֪С��վ������������A��5.7��C�����������������Ϊ75�㣬С�����۾������ľ���DCΪ1.72�ף������С������ķ���AB�ĸ߶ȣ�����ȷ��1�ף��ο�����![]() ��1.732��
��1.732�� ![]() ��1.414��
��1.414��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������Ƕ���ڵ���Ҫϰ�ף�ij�м�����֧���۶��ڶ�����ڼ���л����۱����������Aʻ���յ�B���������г��У������뿪���ľ���y���ף���ʱ��x�����ӣ��Ķ�Ӧ��ϵ��ͼ��ʾ������ͼ�����������⣺
��1�����A���յ�B֮������Զ��
��2����֧���۶��ȳ�������֧���۶��ȵ����յ㣿
��3���ֱ���ס�����֧���۶ӵ�y��x������ϵʽ��
��4�������۶ӳ����ʱ��ʱ��֧���۶����200�ף�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��P������Ϊ(a��1��5��2a)������������������ľ�����ȣ����P������Ϊ(����)
A.(3��3)B.(3����3)C.(1����1)D.(1��1)��(3����3)
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У����Ƕ���ֱ��y=ax��aΪ������![]() ��a��b��cΪ������a��0���ġ�����ֱ�ߡ�����һ���������������ϣ�����һ��������y���ϵ�������Ϊ�䡰���������Ρ���
��a��b��cΪ������a��0���ġ�����ֱ�ߡ�����һ���������������ϣ�����һ��������y���ϵ�������Ϊ�䡰���������Ρ���
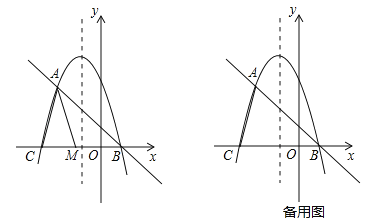
��֪������![]() ���䡰����ֱ�ߡ�����A��B���㣨��A�ڵ�B����ࣩ����x�Ḻ���ύ�ڵ�C��
���䡰����ֱ�ߡ�����A��B���㣨��A�ڵ�B����ࣩ����x�Ḻ���ύ�ڵ�C��
��1����գ��������ߵġ�����ֱ�ߡ��Ľ���ʽΪ ����A������Ϊ ����B������Ϊ ��
��2����ͼ����MΪ�߶�CB��һ���㣬����ACM��AM����ֱ��Ϊ�Գ��ᷭ�ۣ���C�ĶԳƵ�ΪN������AMNΪ�������ߵġ����������Ρ������N�����ꣻ
��3������E�������ߵĶԳ������˶�ʱ���ڸ������ߵġ�����ֱ�ߡ��ϣ��Ƿ���ڵ�F��ʹ���Ե�A��C��E��FΪ������ı���Ϊƽ���ı��Σ������ڣ���ֱ��д����E��F�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com