
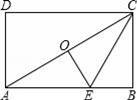
如图,点O是矩形ABCD的中心,E是AB上的点,沿CE折叠后,点B恰好与点O重合,若BC=3,则折痕CE的长为( )


A.
 B.
B.


 C.
C.
 D.6
D.6
A【考点】翻折变换(折叠问题);勾股定理.
【分析】先根据图形翻折变换的性质求出AC的长,再由勾股定理及等腰三角形的判定定理即可得出结论.
【解答】解:∵△CEO是△CEB翻折而成,
∴BC=OC,BE=OE,∠B=∠COE=90°,
∴EO⊥AC,
∵O是矩形ABCD的中心,
∴OE是AC的垂直平分线,AC=2BC=2×3=6,
∴AE=CE,
在Rt△ABC中,AC2=AB2+BC2,即62=AB2+32,解得AB=3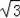
 ,
,
在Rt△AOE中,设OE=x,则AE=3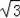
 ﹣x,
﹣x,
AE2=AO2+OE2,即(3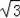
 ﹣x)2=32+x2,解得x=
﹣x)2=32+x2,解得x=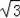
 ,
,
∴AE=EC=3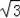
 ﹣
﹣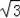
 =2
=2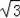
 .
.
故选:A.

【点评】本题考查的是翻折变换,熟知折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等的知识是解答此题的关键.


科目:初中数学 来源: 题型:
如图,“赵爽弦图”是由四个全等的直角三角形与中间一个小正方形拼成的一个大正方形,随机在大正方形及其内部区域投针.若针扎到小正方形(阴影部分)的概率是
 ,则大、小两个正方形的边长之比是 .
,则大、小两个正方形的边长之比是 .


查看答案和解析>>
科目:初中数学 来源: 题型:
一个不透明的口袋中装有4个分别标有数字﹣1,﹣2,3,4的小球,它们的形状、大小完全相同.小红先从口袋中随机摸出一个小球记下数字为x;小颖在剩下的3个小球中随机摸出一个小球记下数字为y.
(1)小红摸出标有数字3的小球的概率是 ;
(2)请用列表法或画树状图的方法表示出由x,y确定的点P(x,y)所有可能的结果;
(3)若规定:点P(x,y)在第一象限或第三象限小红获胜;点P(x,y)在第二象限或第四象限则小颖获胜.请分别求出两人获胜的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com