
如图(1)所示小明剪了一个等腰梯形ABCD,其中AD∥BC,AB=CD;又剪了一个等边三角形EFG,同座位的小华拿过来拼成如图(2)所示的形状,她发现AD与FG恰好完全重合,于是她用透明胶将梯形ABCD和△EFG粘在一起,并沿EB、EC剪下,小华得到的三角形BEC是什么三角形?请你作出判断并说明理由.

科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
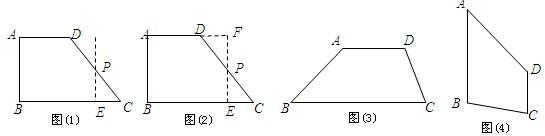
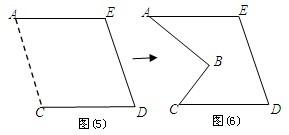
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源:2010年河北省石家庄市第42中学中考数学二模试卷(解析版) 题型:解答题
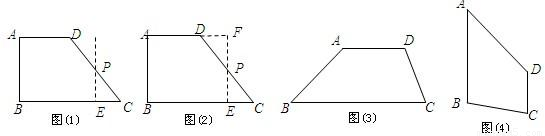
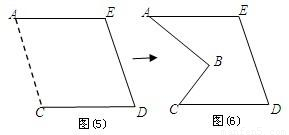
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com