
【题目】方程(x+2)(x﹣3)=x+2的解是 .
科目:初中数学 来源: 题型:
【题目】下列说法正确的有( )
A.近似数1.2×105精确到十分位
B.近似数0.31与0.310精确度相同
C.小明的身高156cm中的数是准确值
D.800万用科学户数法表示为8×106
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某隧道口的横截面是抛物线形,已知路宽AB为6米,最高点离地面的距离OC为5米.以最高点O为坐标原点,抛物线的对称轴为y轴,1米为数轴的单位长度,建立平面直角坐标系,求:(1)以这一部分抛物线为图象的函数解析式,并写出x的取值范围;(2)有一辆宽2.8米,高1米的农用货车(货物最高处与地面AB的距离)能否通过此隧道?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC和△DEC中,∠ABC=∠DEC=90°,连接AD交射线EB于F,AC∥DE,延长CA交射线EB于点G,点F恰好是AD中点。
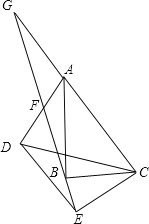
(1)求证:△AFG≌△DFE;
(2)若BC=CE,
①求证:∠ABF=∠DEF;
②若∠BAC=30°,试求∠AFG的度数。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com