
【题目】如图,在△ABC和△DEC中,∠ABC=∠DEC=90°,连接AD交射线EB于F,AC∥DE,延长CA交射线EB于点G,点F恰好是AD中点。
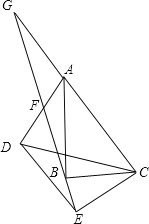
(1)求证:△AFG≌△DFE;
(2)若BC=CE,
①求证:∠ABF=∠DEF;
②若∠BAC=30°,试求∠AFG的度数。
【答案】(1)证明见解析(2)①证明见解析②∠AFG=60°。
【解析】试题分析:
(1)由AG∥DE易得:∠G=∠DEF;由F是AD的中点易得AF=DF,结合∠AFG=∠DFE,即可证得:△AGF≌△DEF;
(2)①由BC=CE可得∠CBE=∠CEB,结合∠ABC=DEC=90°,易得∠ABF+∠CBE=90°,∠CEB+∠DEF=90°,从而可得∠ABF=∠DEF;
②由△AGF≌△DEF可得∠G=∠DEF,AG=DE结合∠ABF=∠DEF,可得:∠ABF=∠G,从而可得:AG=AB,这样即可得到:AB=DE,结合∠ABC=∠DEC=90°,BC=CE即可证得:△ABC≌△DEC,由此可得AC=CD,∠EDC=∠BAC=30°,结合AC∥DE可得∠ACD=∠EDC=30°,从而可得∠CAD=![]() ;由∠BAC=∠G+∠ABG=30°结合∠G=∠ABG易得∠G=15°,结合∠CAD=∠G+∠AFG即可得到∠AFG=60°.
;由∠BAC=∠G+∠ABG=30°结合∠G=∠ABG易得∠G=15°,结合∠CAD=∠G+∠AFG即可得到∠AFG=60°.
试题解析:
(1)∵AG∥DE,点F是AD的中点,
∴∠G=∠DEF,AF=DF,
∵△AGF和△DEF中,
 ,
,
∴△AGF≌△DEF(AAS);
(2)① ∵BC=CE,
∴∠CBE=∠CEB,
∵∠ABC=DEC=90°,
∵∠ABF+∠CBE=90°,∠CEB+∠DEF=90°,
∴∠ABF=∠DEF;
②∵△AGF≌△DEF,
∴∠G=∠DEF,
∵∠ABF=∠DEF,
∴∠ABF=∠G,
∴AG=AB,
∵△AGF≌△DEF,
∴AG=DE,
∴DE=AB,
∵△ABC和△DEC中,
 ,
,
∴△ABC≌△DEC,(SAS)
∴AC=CD,∠BAC=∠EDC,
∵AC∥DE,
∴∠EDC=∠ACD,
∴∠ACD=∠BAC=30°,
∴∠CAD=75°,
∵∠ABF=∠G,∠BAC=30°,
∴∠G=15°,
∵∠CAD=∠G+∠AFG,
∴∠AFG=60°.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图所示,图中的小方格都是边长为1的正方形,△ABC与△A'B'C'是以点O为位似中心的位似图形,它们的顶点都在小正方形的顶点上.
(1)画出位似中心点O;
(2)直接写出△ABC与△A′B'C'的位似比;
(3)以位似中心O为坐标原点,以格线所在直线为坐标轴建立平面直角坐标系,画出△A'B'C'关于点 O中心对称的△A″B″C″,并直接写出△A″B″C″各顶点的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某跳远队甲、乙两名运动员最近10次跳远成绩的平均数为602cm,若甲跳远成绩的方差为S甲2=65.84,乙跳远成绩的方差为S乙2=285.21,则成绩比较稳定的是 . (填“甲”或“乙”)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABE和△ADC是△ABC分别沿AB、AC边翻折得到的,若∠1: ∠2:∠3 = 28 :5 : 3, 则∠4的度数为__________
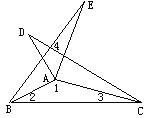
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某文具店今年1月份购进一批笔记本,共2290本,每本进价为10元,该文具店决定从2月份开始进行销售,若每本售价为11元,则可全部售出;且每本售价每增加0.5元,销量就减少15本.
(1)若该种笔记本在2月份的销售量不低于2200本,则2月份售价应不高于多少元?
(2)由于生产商提高工艺,该笔记本的进价提高了10%,文具店为了增加笔记本的销量, 进行了销售调整,售价比2月份在(1)的条件下的最高售价减少了![]() m%,结果3月份的销量比2月份在(1)的条件下的最低销量增加了m%,3月份的销售利润达到 6600元,求m的值.
m%,结果3月份的销量比2月份在(1)的条件下的最低销量增加了m%,3月份的销售利润达到 6600元,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分12分)已知:点E为AB边上的一个动点.
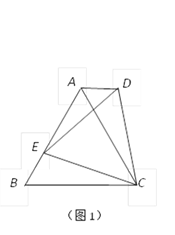
(1)如图1,若△ABC是等边三角形,以CE为边在BC的同侧作等边△DEC ,连结AD.试比较∠DAC与∠B的大小,并说明理由;
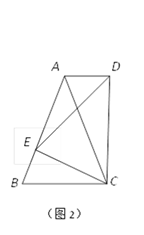
(2)如图2,若△ABC中,AB=AC,以CE为底边在BC的同侧作等腰△DEC ,且
△DEC∽△ABC,连结AD.试判断AD与BC的位置关系,并说明理由;
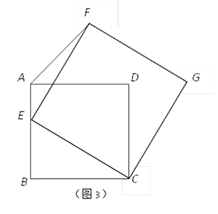
(3)如图3,若四边形ABCD是边长为2的正方形,以CE为边在BC的同侧作正方形ECGF.
①试说明点G一定在AD的延长线上;
②当点E在AB边上由点B运动至点A时,点F随之运动,求点F的运动路径长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com