
【题目】(本题满分12分)已知:点E为AB边上的一个动点.
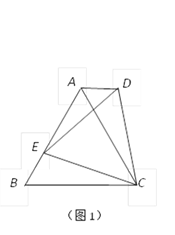
(1)如图1,若△ABC是等边三角形,以CE为边在BC的同侧作等边△DEC ,连结AD.试比较∠DAC与∠B的大小,并说明理由;
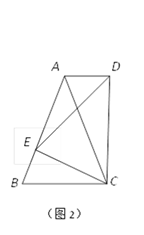
(2)如图2,若△ABC中,AB=AC,以CE为底边在BC的同侧作等腰△DEC ,且
△DEC∽△ABC,连结AD.试判断AD与BC的位置关系,并说明理由;
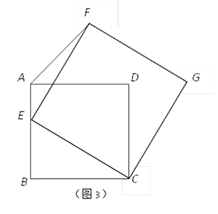
(3)如图3,若四边形ABCD是边长为2的正方形,以CE为边在BC的同侧作正方形ECGF.
①试说明点G一定在AD的延长线上;
②当点E在AB边上由点B运动至点A时,点F随之运动,求点F的运动路径长.
【答案】(1)∠DAC=∠B 理由见解析;(2)AD∥BC 理由见解析;(3)点F的运动路径长为![]() .
.
【解析】解:(1) ∠DAC=∠B 理由如下:
∵△ABC和△DEC都是等边三角形 ∴∠DCE=∠ACB=60° ∴∠BCE=∠ACD
∵BC=AC CE=CD ∴△BCE≌△ACD ∴∠B=∠DAC
(2)AD∥BC 理由如下:
∵△ABC和△DEC都是等腰三角形,且△DEC∽△ABC ∴![]()
∵∠DCE=∠ACB ∴∠DCA=∠ECB ∴△DCA∽△ECB
∴∠DAC=∠EBC=∠ACB ∴AD∥BC
(3)①连结DG,∵四边形ABCD和FECG都是正方形
∴BC=CD CE=CG ∠BCD=∠ECG=90°
∴∠BCE=∠DCG∴△BCE≌△DCG …∴∠B=∠CDG=90°
∵∠ADC=90°∴∠ADC+∠CDG=180°
∴点G一定在AD的延长线上.
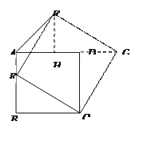
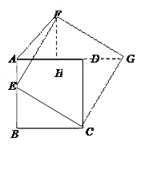
②作FH⊥AG于点H,易证:△FHG≌△GDC≌△EBC
∴FH=BE=DG HG=BC
∴AH=AG-GH=AD+DG-GH= BC+DG-BC=DG=FH
∴△AFH是等腰直角三角形
∴∠FAG=45°
∴点F的运动路径长=AC=![]() .
.


 发散思维新课堂系列答案
发散思维新课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC和△DEC中,∠ABC=∠DEC=90°,连接AD交射线EB于F,AC∥DE,延长CA交射线EB于点G,点F恰好是AD中点。
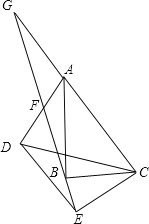
(1)求证:△AFG≌△DFE;
(2)若BC=CE,
①求证:∠ABF=∠DEF;
②若∠BAC=30°,试求∠AFG的度数。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB=AD,添加下列一个条件后,仍无法确定△ABC≌△ADC的是( ) 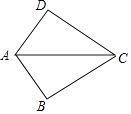
A.BC=CD
B.∠BAC=∠DAC
C.∠B=∠D=90°
D.∠ACB=∠ACD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从边长为a的正方形中剪掉一个边长为b的正方形(如图1),然后将剩余部分拼成一个长方形(如图2). 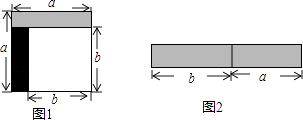
(1)上述操作能验证的等式是(填A或B)
A.a2﹣2ab+b2=(a﹣b)2
B.a2﹣b2=(a+b)(a﹣b)
(2)应用你从(1)中选出的等式,计算: (1﹣ ![]() )(1﹣
)(1﹣ ![]() )(1﹣
)(1﹣ ![]() )…(1﹣
)…(1﹣ ![]() )(1﹣
)(1﹣ ![]() ).
).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com