练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，AB=AD，添加下列一个条件后，仍无法确定△ABC≌△ADC的是（ ）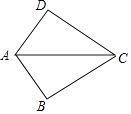
    A.BC=CD
    B.∠BAC=∠DAC
    C.∠B=∠D=90°
    D.∠ACB=∠ACD

    【答案】D
    【解析】解：A、AB=AD、AC=AC、BC=CD，符合全等三角形的判定定理SSS，能推出△ABC≌△ADC，故本选项不符合题意； B、AB=AD、∠BAC=∠DAC、AC=AC，符合全等三角形的判定定理SAS，能推出△ABC≌△ADC，故本选项不符合题意；
    C、AB=AD、AC=AC、∠B=∠D=90°，符合全等三角形的判定定理HL，能推出△ABC≌△ADC，故本选项不符合题意；
    D、AB=AD、AC=AC、∠ACB=∠ACD，不符合全等三角形的判定定理，不能推出△ABC≌△ADC，故本选项符合题意；
    故选D．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】某文具店今年1月份购进一批笔记本，共2290本，每本进价为10元，该文具店决定从2月份开始进行销售，若每本售价为11元，则可全部售出；且每本售价每增加0.5元，销量就减少15本．

    （1）若该种笔记本在2月份的销售量不低于2200本，则2月份售价应不高于多少元？

    （2）由于生产商提高工艺，该笔记本的进价提高了10%，文具店为了增加笔记本的销量， 进行了销售调整，售价比2月份在（1）的条件下的最高售价减少了m%，结果3月份的销量比2月份在（1）的条件下的最低销量增加了m%，3月份的销售利润达到 6600元，求m的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（本题满分12分）已知：点E为AB边上的一个动点.

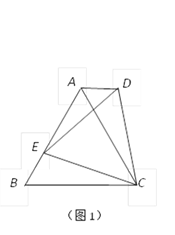
    （1）如图1，若△ABC是等边三角形，以CE为边在BC的同侧作等边△DEC ，连结AD.试比较∠DAC与∠B的大小，并说明理由；

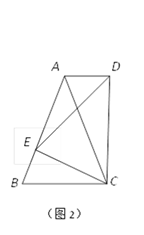
    （2）如图2，若△ABC中，AB=AC，以CE为底边在BC的同侧作等腰△DEC ，且

    △DEC∽△ABC，连结AD.试判断AD与BC的位置关系，并说明理由；

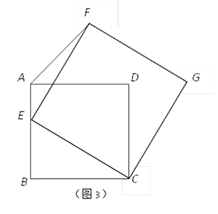
    （3）如图3，若四边形ABCD是边长为2的正方形，以CE为边在BC的同侧作正方形ECGF.

    ①试说明点G一定在AD的延长线上；

    ②当点E在AB边上由点B运动至点A时，点F随之运动，求点F的运动路径长.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列计算正确的是（ ）
    A.﹣3a+4a=﹣7a
    B.4m+2n=6mn
    C.5x+4x=20x2
    D.6xy3﹣2xy3=4xy3

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如果两个三角形的两边及其中一边的对角对应相等，那么这两个三角形全等，其逆命题是_______________________，这个逆命题是________命题．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图①，已知AC是矩形纸片ABCD的对角线，AB =3，BC =4．现将矩形ABCD沿对角线AC剪开，再把△ABC沿着AD方向平移，得到图②中△A′BC′，当四边形A′ECF是菱形时，平移距离AA′的长是___________.

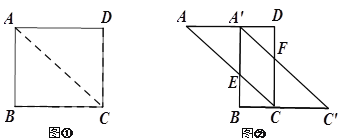
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】定义：三边长和面积都是整数的三角形称为“整数三角形”.

    数学学习小组的同学从32根等长的火柴棒（每根长度记为1个单位）中取出若干根，首尾依次相接组成三角形，进行探究活动.

    小亮用12根火柴棒，摆成如图所示的“整数三角形”；

    小颖分别用24根和30根火柴棒摆出直角“整数三角形”；

    小辉受到小亮、小颖的启发，分别摆出三个不同的等腰“整数三角形”.

    ⑴请你画出小颖和小辉摆出的“整数三角形”的示意图；

    ⑵你能否也从中取出若干根，按下列要求摆出“整数三角形”，如果能，请画出示意图；如果不能，请说明理由.

    ①画出等边“整数三角形”；

    ②摆出一个非特殊（既非直角三角形，也非等腰三角形）“整数三角形”.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】三个连续正整数的和不大于12．这样的正整数有__________组．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，AC和BD相交于O点，若OA=OD，用“SAS”证明△AOB≌△DOC还需（ ）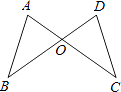
    A.AB=DC
    B.OB=OC
    C.∠C=∠D
    D.∠AOB=∠DOC

    查看答案和解析>>

    同步练习册答案