
����Ŀ������ڼ䣬ij�����̵��Ƴ����ۼ���Ʒ�����֪����Ʒÿ���Ľ�����Ϊ30Ԫ�����г����з��֣����ü���Ʒ�����۵���Ϊ40Ԫʱ��ÿ�������280���������۵���ÿ����1Ԫ��ÿ�����������������10�������������������ܶ�����ɱ���
��1�����ü���Ʒ�����۵���Ϊ45Ԫʱ������������Ϊ�� ����
��2�����ü���Ʒ�����۵���Ϊ����Ԫʱ���ü���Ʒ�ĵ�������������2610Ԫ��
��3�����ü���Ʒ�����۵��۶�Ϊ����Ԫʱ���ü���Ʒ�ĵ�����������ﵽ���ֵ������������
���𰸡���1��230����2�����ü���Ʒ�����۵���Ϊ59Ԫʱ���ò�Ʒ�ĵ�������������2610Ԫ����3�����ü���Ʒ�����۵��۶�Ϊ49Ԫʱ���ü���Ʒ�ĵ�����������ﵽ���ֵ���������Ϊ3610Ԫ��
��������
��1�������۵���Ϊ45Ԫʱ����40Ԫ������5Ԫ���Ӷ��ɵ�ÿ��������������ٵ����������ɵó��𰸣�
��2�������Ʒ�����۵���ΪxԪ���������Ӧ�ĵ�������������ٸ��ݡ��������������ܶ�����ɱ�������������⼴�ɣ�
��3�������Ʒ�����۵���ΪxԪ������Ʒ�ĵ�����������ΪyԪ��ͬ�⣨2����˼·���ɵó�y����x��һ�����κ����������ö��κ��������ʼ��ɵã�
��1��������ã�![]() ������
������
�ʴ�Ϊ��230��
��2����ü���Ʒ�����۵���ΪxԪ![]() �������������Ϊ
�������������Ϊ![]() ��
��
��ˣ������ܶ�Ϊ![]() Ԫ�������ɱ�Ϊ
Ԫ�������ɱ�Ϊ![]() Ԫ
Ԫ
������ã�![]()
�����ã�![]()
��ã�![]() ���������⣬��ȥ����
���������⣬��ȥ����![]()
�𣺵��ü���Ʒ�����۵���Ϊ59Ԫʱ���ò�Ʒ�ĵ�������������2610Ԫ��
��3����ü���Ʒ�����۵���ΪxԪ![]() ��������������ΪyԪ�������������Ϊ
��������������ΪyԪ�������������Ϊ![]() ��
��
ͬ����2���ɵã�![]()
![]()
![]()
�ɶ��κ��������ʿ�֪�������ߵĿ������£���![]() ʱ��yȡ�����ֵ�����ֵΪ
ʱ��yȡ�����ֵ�����ֵΪ![]() Ԫ
Ԫ
�𣺵��ü���Ʒ�����۵��۶�Ϊ49Ԫʱ���ü���Ʒ�ĵ���������������ﵽ���ֵ���������Ϊ3610Ԫ��


 ǧ�������������ĩ�����Ծ�����ϵ�д�
ǧ�������������ĩ�����Ծ�����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
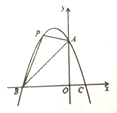
����Ŀ����֪:��ͼ��������![]() ��������ֱ��ڵ�
��������ֱ��ڵ�![]() �� ��
�� ��![]() ���߶�
���߶�![]() �Ϸ��������ϵ�һ�����㣬
�Ϸ��������ϵ�һ�����㣬
(1)�������߽���ʽ:
(2)����![]() �˶���ʲôλ��ʱ��
�˶���ʲôλ��ʱ��![]() ��������?
��������?
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ƽ��ֱ������ϵ�У�һ�κ���y��x��1��ͼ����x�ᣬy��ֱ��ڵ�A��B���뷴��������y��![]() ��ͼ���ڵ�C��D��CE��x���ڵ�E��
��ͼ���ڵ�C��D��CE��x���ڵ�E��![]() ��
��
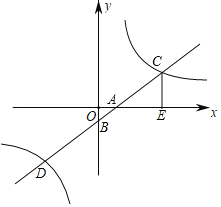
��1�����������ı���ʽ���D�����ꣻ
��2����CEΪ����ECMN����M��һ�κ���y��x��1��ͼ���ϣ����M�ĺ�����Ϊa������MN�뷴��������y��![]() ��ͼ���й�����ʱ����a��ȡֵ��Χ��
��ͼ���й�����ʱ����a��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ,A��B�Ǻ���![]() ͼ���Ϲ���ԭ��ԳƵ�����,��BC//x��,AC//y��,��ABC�������ΪS,��( )
ͼ���Ϲ���ԭ��ԳƵ�����,��BC//x��,AC//y��,��ABC�������ΪS,��( )
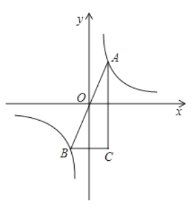
A.S=2B.S=4C.S=8D.S=1
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ,������ABCD�ı߳�Ϊ4,E��BC�ߵ��е�,��P������AD��,��P��PF��AE��F.
(1)��֤:![]() ;
;
(2)����P������AD���˶�ʱ,��PA=X,�Ƿ����ʵ��x,ʹ��P,F,EΪ�����������Ҳ���ABE����?������,�����x��ֵ;��������,˵������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
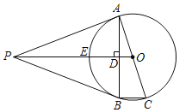
����Ŀ����ͼ��PA�ǡ�O�����ߣ��е�ΪA��AC�ǡ�O��ֱ��������OP����O��E����A����AB��PO�ڵ�D������O��B������BC��PB��
��1����֤��PB�ǡ�O�����ߣ�
��2����֤��EΪ��PAB�����ģ�
��3����cos��PAB��![]() ��BC��1����PO�ij���
��BC��1����PO�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
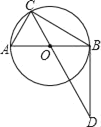
����Ŀ����ͼ��AB����O��ֱ����CΪ��O��һ�㣬��D��CO���ӳ����ϣ�����BD����֪BC��BD��AB��4��
��1����BC��2![]() ����֤��BD����O�����ߣ�
����֤��BD����O�����ߣ�
��2��BC��3����CD�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
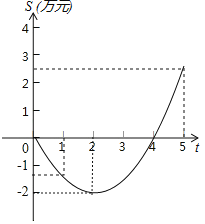
����Ŀ��ij��˾�Ƴ���һ�ָ�Ч������ϴ����Ʒ��������к�˾�����˴ӿ���ӯ���Ĺ��̣�����Ķ��κ���ͼ���֣��̻��˸ù�˾���������������S����Ԫ��������ʱ��t���£�֮��Ĺ�ϵ����ǰt���µ������ܺ�S��t֮��Ĺ�ϵ����
����ͼ���ṩ����Ϣ������������⣺
��1������֪ͼ���ϵ��������꣬���ۻ�����S����Ԫ����ʱ��t���£�֮��ĺ�����ϵʽ��
��2�����8���¹�˾���������Ƕ�����Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������![]() ��x�ύ�ڵ�A����1��0�����������꣨1��n������y��Ľ����ڣ�0��3������0��4��֮�䣨�����˵㣩�������н��ۣ���abc��0����3a+b��0���۩�
��x�ύ�ڵ�A����1��0�����������꣨1��n������y��Ľ����ڣ�0��3������0��4��֮�䣨�����˵㣩�������н��ۣ���abc��0����3a+b��0���۩�![]() ��a����1����a+b��am2+bm��mΪ����ʵ��������һԪ���η���
��a����1����a+b��am2+bm��mΪ����ʵ��������һԪ���η���![]() ����������ȵ�ʵ������������ȷ���У�������
����������ȵ�ʵ������������ȷ���У�������

A. 2�� B. 3�� C. 4�� D. 5��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com