
【题目】如图,A、B是函数![]() 图象上关于原点对称的两点,且BC//x轴,AC//y轴,△ABC的面积记为S,则( )
图象上关于原点对称的两点,且BC//x轴,AC//y轴,△ABC的面积记为S,则( )
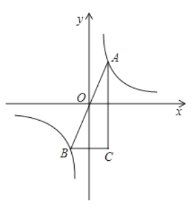
A.S=2B.S=4C.S=8D.S=1
科目:初中数学 来源: 题型:
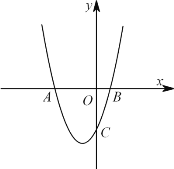
【题目】如图,抛物线![]() 与
与![]() 轴交于
轴交于![]() 、
、![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() .
.
(1)求点![]() 、
、![]() 、
、![]() 的坐标;
的坐标;
(2)若点![]() 在
在![]() 轴的上方,以
轴的上方,以![]() 、
、![]() 、
、![]() 为顶点的三角形与
为顶点的三角形与![]() 全等,平移这条抛物线,使平移后的抛物线经过点
全等,平移这条抛物线,使平移后的抛物线经过点![]() 与点
与点![]() ,请你写出平移过程,并说明理由。
,请你写出平移过程,并说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】只有1和它本身两个因数且大于1的正整数叫做素数.我国数学家陈景润哥德巴赫猜想的研究中取得了世界领先的成果.哥德巴赫猜想是“每个大于2的偶数都表示为两个素数的和”.如20=3+17.
(1)从7、11、19、23这4个素数中随机抽取一个,则抽到的数是7的概率是 ;
(2)从7、11、19、23这4个素数中随机抽取1个数,再从余下的3个数中随机抽取1个数,用画树状图或列表的方法,求抽到的两个素数之和等于30的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读,我们可以用换元法解简单的高次方程,解方程x4﹣3x2+2=0时,可设y=x2,则原方程可比为y2+3y+2=0,解之得y1=2,y2=1,当y1=2时,则x2=2,即x1=![]() ,x2=﹣
,x2=﹣![]() ;当y2=1时,即x2=1,则x1=1,x2=﹣1,故原方程的解为x1=
;当y2=1时,即x2=1,则x1=1,x2=﹣1,故原方程的解为x1=![]() ,x2=﹣
,x2=﹣![]() ,x3=1,x4=﹣1,仿照上面完成下面解答:
,x3=1,x4=﹣1,仿照上面完成下面解答:
(1)已知方程(2x2+1)2+2x2﹣3=0,设y=2x2+1,则原方程可化为_______.
(2)仿照上述解法解方程:(x2﹣2x)2﹣3x2+6x=0.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 的图与y轴分别交于点A,且反比例函数
的图与y轴分别交于点A,且反比例函数![]() 的图象在第一象限内的交点为M.
的图象在第一象限内的交点为M.
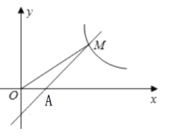
(1)求点M的坐标.
(2)在x轴上是否存在点P,使AM⊥MP?若存在,求出点P的坐标;若不存在,说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】暑假期间,某景区商店推出销售纪念品活动,已知纪念品每件的进货价为30元,经市场调研发现,当该纪念品的销售单价为40元时,每天可销售280件;当销售单价每增加1元,每天的销售数量将减少10件.(销售利润=销售总额﹣进货成本)
(1)若该纪念品的销售单价为45元时,则当天销售量为 件.
(2)当该纪念品的销售单价为多少元时,该纪念品的当天销售利润是2610元.
(3)当该纪念品的销售单价定为多少元时,该纪念品的当天销售利润达到最大值?求此最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
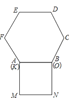
【题目】已知正方形![]() 和正六边形
和正六边形![]() 边长均为1,如图所示,把正方形放置在正六边形外,使
边长均为1,如图所示,把正方形放置在正六边形外,使![]() 边与
边与![]() 边重合,按下列步骤操作:将正方形在正六边形外绕点
边重合,按下列步骤操作:将正方形在正六边形外绕点![]() 逆时针旋转,使
逆时针旋转,使![]() 边与
边与![]() 边重合,完成第一次旋转;再绕点
边重合,完成第一次旋转;再绕点![]() 逆时针旋转,使
逆时针旋转,使![]() 边与
边与![]() 边重合,完成第二次旋转;此时点
边重合,完成第二次旋转;此时点![]() 经过路径的长为___________.若按此方式旋转,共完成六次,在这个过程中点
经过路径的长为___________.若按此方式旋转,共完成六次,在这个过程中点![]() ,
,![]() 之间距离的最大值是______.
之间距离的最大值是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
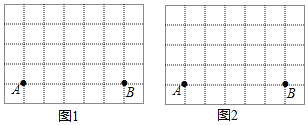
【题目】如图是两张形状,大小完全相同的方格纸,方格纸中的每个小正方形的边长均为1,点A,B均在小正方形的顶点上.
(1)在图1中画出面积为5的△ABC,且△ABC中有一个角为45°;
(2)在图2中画出△ABD,且∠ADB=90°并直接写出△ABD的周长.(C,D都在方格顶点上,每幅图画出一种情况即可)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com