练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

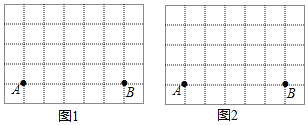
    【题目】如图是两张形状，大小完全相同的方格纸，方格纸中的每个小正方形的边长均为1，点A，B均在小正方形的顶点上．

    （1）在图1中画出面积为5的△ABC，且△ABC中有一个角为45°；

    （2）在图2中画出△ABD，且∠ADB＝90°并直接写出△ABD的周长．（C，D都在方格顶点上，每幅图画出一种情况即可）

    【答案】（1）见解析；（2）画图见解析，5+3.

    【解析】

    （1）利用网格特点：正方形对角线与网格线的夹角即为45°，从而可画出45°的锐角，再根据三角形的面积公式确定点C的位置即可；

    （2）根据勾股定理的逆定理即可画出图形，计算三角形的三边即可得出其周长．

    解：（1）如图1，△ABC即为所求，∠A＝45°；

    （2）如图2，△ABD即为所求，△ABD的周长＝5+3．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图,A、B是函数图象上关于原点对称的两点,且BC//x轴,AC//y轴,△ABC的面积记为S,则( )

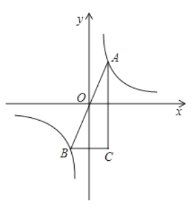
    A.S=2B.S=4C.S=8D.S=1

    查看答案和解析>>

    科目：初中数学 来源： 题型：

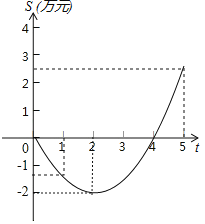
    【题目】某公司推出了一种高效环保型洗涤用品，年初上市后，公司经历了从亏损到盈利的过程，下面的二次函数图象（部分）刻画了该公司年初以来积累利润S（万元）与销售时间t（月）之间的关系（即前t个月的利润总和S与t之间的关系）．

    根据图象提供的信息，解答下列问题：

    （1）由已知图象上的三点坐标，求累积利润S（万元）与时间t（月）之间的函数关系式；

    （2）求第8个月公司所获利润是多少万元？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，正方形的顶点、在圆上，若，圆的半径为2，则阴影部分的面积是__________．（结果保留根号和）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】 如图，已知抛物线与轴交于两点，与轴交于点.

    求点的坐标;

    点是此抛物线上的点，点是其对称轴上的点，求以为顶点的平行四边形的面积;

    查看答案和解析>>

    科目：初中数学 来源： 题型：

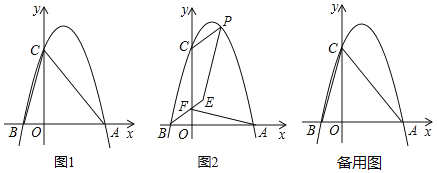
    【题目】已知抛物线的解析式y＝ax2+bx+3与x轴交于A、B两点，点B的坐标为（﹣1，0）抛物线与y轴正半轴交于点C，△ABC面积为6．

    （1）如图1，求此抛物线的解析式；

    （2）P为第一象限抛物线上一动点，过P作PG⊥AC，垂足为点G，设点P的横坐标为t，线段PG的长为d，求d与t之间的函数关系式，并直接写出自变量t的取值范围；

    （3）如图2，在（2）的条件下，过点B作CP的平行线交y轴上一点F，连接AF，在BF的延长线上取点E，连接PE，若PE＝AF，∠AFE+∠BEP＝180°，求点P的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，抛物线 与x轴交于点A（﹣1，0），顶点坐标（1，n），与y轴的交点在（0，3），（0，4）之间（包含端点），则下列结论：①abc＞0；②3a+b＜0；③﹣≤a≤﹣1；④a+b≥am2+bm（m为任意实数）；⑤一元二次方程 有两个不相等的实数根，其中正确的有（　　）

    A. 2个 B. 3个 C. 4个 D. 5个

    查看答案和解析>>

    科目：初中数学 来源： 题型：

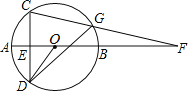
    【题目】如图，AB是⊙O的直径，弦CD⊥AB于点E，点G为弧BC上一动点，CG与AB的延长线交于点F，连接OD．

    （1）判定∠AOD与∠CGD的大小关系为　 　，并求证：GB平分∠DGF．

    （2）在G点运动过程中，当GD＝GF时，DE＝4，BF＝，求⊙O的半径．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，∠MON=60°，OF平分∠MON，点A在射线OM上， P，Q是射线ON上的两动点，点P在点Q的左侧，且PQ=OA，作线段OQ的垂直平分线，分别交OM，OF，ON于点D，B，C，连接AB，PB．

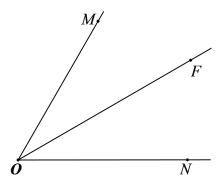
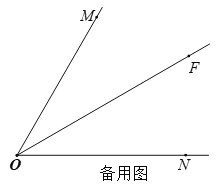
    （1）依题意补全图形；

    （2）判断线段 AB，PB之间的数量关系，并证明；

    （3）连接AP，设，当P和Q两点都在射线ON上移动时，是否存在最小值？若存在，请直接写出的最小值；若不存在，请说明理由．

    查看答案和解析>>

    同步练习册答案