
����Ŀ����ͼ����MON=60����OFƽ�֡�MON����A������OM�ϣ� P��Q������ON�ϵ������㣬��P�ڵ�Q����࣬��PQ=OA�����߶�OQ�Ĵ�ֱƽ���ߣ��ֱ�OM��OF��ON�ڵ�D��B��C������AB��PB��
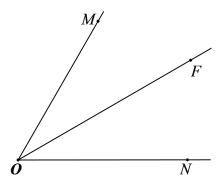
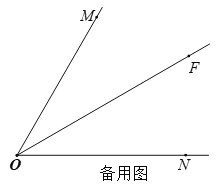
��1�������ⲹȫͼ�Σ�
��2���ж��߶� AB��PB֮���������ϵ����֤����
��3������AP����![]() ����P��Q���㶼������ON���ƶ�ʱ��
����P��Q���㶼������ON���ƶ�ʱ��![]() �Ƿ������Сֵ�������ڣ���ֱ��д��
�Ƿ������Сֵ�������ڣ���ֱ��д��![]() ����Сֵ���������ڣ���˵�����ɣ�
����Сֵ���������ڣ���˵�����ɣ�
���𰸡���1����ȫͼ�μ������� ��2��AB=PB��֤������������3�����ڣ�![]() ��
��
��������
��1���������ⲹȫͼ����ͼ1��
��2�����ۣ�AB=PB������BQ��ֻҪ֤����AOB�ա�PQB���ɽ�����⣻
��3������BQ��ֻҪ֤����ABP�ס�OBQ�������Ƴ�![]() ���ɡ�AOB=30�����Ƴ���BA��OMʱ��
���ɡ�AOB=30�����Ƴ���BA��OMʱ��![]() ��ֵ��С����СֵΪ
��ֵ��С����СֵΪ![]() ���ɴ˼��ɽ�����⣮
���ɴ˼��ɽ�����⣮
�⣺��1����ͼ1��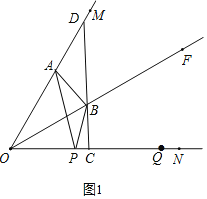
��2��AB=PB��
֤������ͼ������BQ��
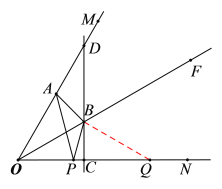
��BC�Ĵ�ֱƽ��OQ��
�� OB =BQ��
���BOP=��BQP��
�֡� OFƽ�֡�MON��
���AOB = ��BOP��
���AOB = ��BQP��
�֡�PQ=OA��
�� ��AOB�ա�PQB��
��AB=PB��
��3�����ߡ�AOB�ա�PQB��
���OAB=��BPQ��
�ߡ�OPB+��BPQ=180����
���OAB+��OPB=180������AOP+��ABP=180����
�ߡ�MON=60����
���ABP=120����
��BA=BP��
���BAP=��BPA=30����
��BO=BQ��
���BOQ=��BQO=30����
���ABP�ס�OBQ��
��![]() ��
��
�ߡ�AOB=30����
�൱BA��OMʱ��![]() ��ֵ��С����СֵΪ
��ֵ��С����СֵΪ![]() ��
��
��k=![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
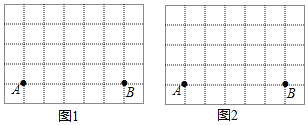
����Ŀ����ͼ��������״����С��ȫ��ͬ�ķ���ֽ������ֽ�е�ÿ��С�����εı߳���Ϊ1����A��B����С�����εĶ����ϣ�
��1����ͼ1�л������Ϊ5����ABC������ABC����һ����Ϊ45����
��2����ͼ2�л�����ABD���ҡ�ADB��90����ֱ��д����ABD���ܳ�����C��D���ڷ����ϣ�ÿ��ͼ����һ��������ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
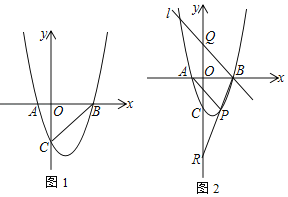
����Ŀ����ͼ1����ƽ��ֱ������ϵ�У�������y��ax2��2x��3a��x�ύ��A��B���㣬��y�ύ��C�㣬OC��OB����PΪ��������һ����
��1���������ߵĽ���ʽ��
��2������P�˶��������߶Գ����Ҳ�ʱ��ͼ2����PC��BC��BP����BCP������BCP�����Ϊs����P�ĺ�����Ϊx����s��![]() ����x��ȡֵ��Χ��
����x��ȡֵ��Χ��
��3������P�˶�����������ʱ����AP��BP��BP��y���ڵ�R����B��ֱ��l��AP��y���ڵ�Q���ʣ�QR��OC֮���Ƿ����ȷ����������ϵ�������ڣ��������֤�����������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ij��ũ��Ʒ�ijɱ�ÿǧ��20Ԫ�����鷢�֣��ò�Ʒÿ��������y��ǧ�ˣ������۵���x��Ԫ/ǧ�ˣ��������¹�ϵ��![]() ��������ũ��Ʒ����������ΪwԪ��
��������ũ��Ʒ����������ΪwԪ��
��1����w��x֮��ĺ�����ϵʽ��
��2���ò�Ʒ���ۼ۶�Ϊ����Ԫʱ��ÿ����������������������Ƕ���Ԫ��
��3����۲��Ź涨���ֲ�Ʒ�����ۼ۲��ø���ÿǧ��28Ԫ����ũ���������ֲ�Ʒ��������ÿ����150Ԫ���������ۼ�Ӧ��Ϊÿǧ�˶���Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������ƶ�֧���ѳ�Ϊ��Ҫ֧����ʽ֮һ��Ϊ�˽�ijУ800��ѧ���ϸ���A��B�����ƶ�֧����ʽ��ʹ���������ȫУѧ���������ȡ��100�ˣ�����������A��B����֧����ʽ����ʹ������5�ˣ������н�ʹ��A�ͽ�ʹ��B��ѧ����֧�����ֲ�������£�
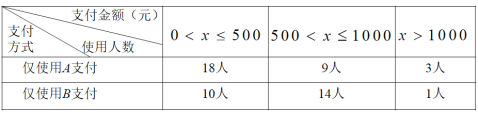
�������ĸ��ƶϣ�
�ٴ�ȫУѧ���������ȡ1�ˣ���ѧ���ϸ��½�ʹ��A֧���ĸ���Ϊ0.3��
�ڴ�ȫУѧ���������ȡ1�ˣ���ѧ���ϸ���A��B����֧����ʽ��ʹ�õĸ���Ϊ0.45��
�۹���ȫУ��ʹ��B֧����ѧ������Ϊ200�ˣ�
����100��ѧ���У��ϸ��½�ʹ��A�ͽ�ʹ��B֧����ѧ��֧��������λ��Ϊ800Ԫ��
���к����ƶϵ�����ǣ� ��
A.�٢�B.�٢�C.�٢�D.�ڢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������С��ͬѧ��Ƶ����������εĸ������ij߹���ͼ�Ĺ��̣�
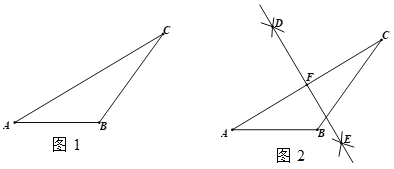
��֪����ͼ1����ABC��
������AB���ϵĸ��ߣ�
��������ͼ2��
�ٷֱ���A��CΪԲ�ģ�����![]() ��
��
Ϊ�뾶�����������ֱ��ڵ�D��E��
�� ��ֱ��DE����AC�ڵ�F��
�� �Ե�FΪԲ�ģ�FA��Ϊ�뾶��Բ����AB���ӳ����ڵ�M��
�� ����CM��
��CM Ϊ����AB���ϵĸ��ߣ�
����������ͼ���̣��ش����⣺
��1����ֱ�ߺ�Բ�棬��ȫͼ2�е�ͼ�Σ�
��2����������֤����
֤��������DA��DC��EA��EC��
������ͼ��֪DA=DC =EA=EC��
��DE���߶�AC�Ĵ�ֱƽ���ߣ�
��FA=FC ��
��AC�ǡ�F��ֱ����
���AMC=______����___________________________________���������ݣ���
��CM��AB��
��CM����AB���ϵĸ��ߣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
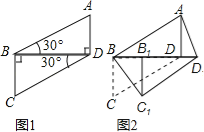
����Ŀ��������ȫ�ȵĺ�30���ǵ����dz���ͼ1�ڷ���һ����϶�ֱ�DZ�Ϊ1����ͼ2����Rt��BCD������BD����ƽ�ƣ���ƽ�ƵĹ����У�����B���ƶ�����Ϊ ʱ���ı�ABC1D1Ϊ���Σ�����B���ƶ�����Ϊ ʱ���ı���ABC1D1Ϊ���Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
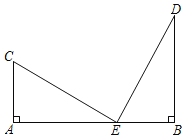
����Ŀ����ͼ����֪BD��AB�ڵ�B��AC��AB�ڵ�A����BD��3��AC��2��AB��m�����߶�AB����һ��E��ʹ��BDE���ACE���ƣ��������ĵ�E����ֻ����������m��ֵ��______
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij����̵���ÿ��60ԪΪ�ɱ�����һ��������ߣ���ÿ��100Ԫ�ļ۸�������ÿ�������20����Ϊ���������ۣ�����ӯ����������ٿ�棬�̵������ȡ�ʵ��Ľ��۴�ʩ�������鷢�֣���ÿ�����ÿ����1Ԫ����ÿ��ɶ���2��.
(1)���̵����ÿ��ӯ��1200Ԫ��ÿ����ߵ��ۼ�Ӧ��Ϊ����Ԫ��
(2)���̵�Ϊ��Ч�����ÿ����ߵ��ۼ۶�Ϊ����Ԫʱ���̵�ÿ��ӯ����ࣿ���ӯ������Ԫ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com