
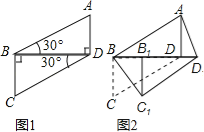
【题目】将两块全等的含30°角的三角尺如图1摆放在一起,设较短直角边为1,如图2,将Rt△BCD沿射线BD方向平移,在平移的过程中,当点B的移动距离为 时,四边ABC1D1为矩形;当点B的移动距离为 时,四边形ABC1D1为菱形.
 全能测控一本好卷系列答案
全能测控一本好卷系列答案科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与x轴交于点A(﹣1,0),顶点坐标(1,n),与y轴的交点在(0,3),(0,4)之间(包含端点),则下列结论:①abc>0;②3a+b<0;③﹣
与x轴交于点A(﹣1,0),顶点坐标(1,n),与y轴的交点在(0,3),(0,4)之间(包含端点),则下列结论:①abc>0;②3a+b<0;③﹣![]() ≤a≤﹣1;④a+b≥am2+bm(m为任意实数);⑤一元二次方程
≤a≤﹣1;④a+b≥am2+bm(m为任意实数);⑤一元二次方程![]() 有两个不相等的实数根,其中正确的有( )
有两个不相等的实数根,其中正确的有( )

A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 过点
过点![]() ,交x轴于A,B两点
,交x轴于A,B两点![]() 点A在点B的左侧
点A在点B的左侧![]() .
.

![]() 求抛物线的解析式,并写出顶点M的坐标;
求抛物线的解析式,并写出顶点M的坐标;
![]() 连接OC,CM,求
连接OC,CM,求![]() 的值;
的值;
![]() 若点P在抛物线的对称轴上,连接BP,CP,BM,当
若点P在抛物线的对称轴上,连接BP,CP,BM,当![]() 时,求点P的坐标.
时,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠MON=60°,OF平分∠MON,点A在射线OM上, P,Q是射线ON上的两动点,点P在点Q的左侧,且PQ=OA,作线段OQ的垂直平分线,分别交OM,OF,ON于点D,B,C,连接AB,PB.
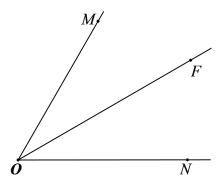
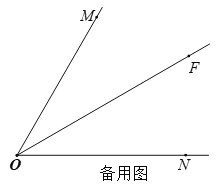
(1)依题意补全图形;
(2)判断线段 AB,PB之间的数量关系,并证明;
(3)连接AP,设![]() ,当P和Q两点都在射线ON上移动时,
,当P和Q两点都在射线ON上移动时,![]() 是否存在最小值?若存在,请直接写出
是否存在最小值?若存在,请直接写出![]() 的最小值;若不存在,请说明理由.
的最小值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
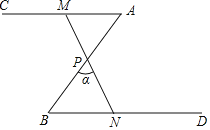
【题目】如图,∠A=∠B=50°,P为AB中点,点M为射线AC上(不与点A重合)的任意点,连接MP,并使MP的延长线交射线BD于点N,设∠BPN=α.
(1)求证:△APM≌△BPN;
(2)当MN=2BN时,求α的度数;
(3)若△BPN的外心在该三角形的内部,直接写出α的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】端午节放假期间,小明和小华准备到宜宾的蜀南竹海(记为A)、兴文石海(记为B)、夕佳山民居(记为C)、李庄古镇(记为D)的一个景点去游玩,他们各自在这四个景点中任选一个,每个景点都被选中的可能性相同.
(1)小明选择去蜀南竹海旅游的概率为 .
(2)用树状图或列表的方法求小明和小华都选择去兴文石海旅游的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为“节能减排,保护环境”,某村计划建造A、B两种型号的沼气池共20个,以解决所有农户的燃料问题.据市场调查:建造A、B两种型号的沼气池各1个,共需费用5万元;建造A型号的沼气池3个,B种型号的沼气池4个,共需费用18万元.
(1)求建造A、B两种型号的沼气池造价分别是多少?
(2)设建造A型沼气池x个,总费用为y万元,求y与x之间的函数关系式;若要使投入总费用不超过52万元,至少要建造A型沼气池多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
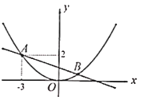
【题目】已知二次函数图象的顶点在原点![]() ,对称轴为
,对称轴为![]() 轴.直线
轴.直线![]() 的图象与二次函数的图象交于点
的图象与二次函数的图象交于点![]() 和点
和点![]() (点
(点![]() 在点
在点![]() 的左侧)
的左侧)
(1)求![]() 的值及直线
的值及直线![]() 解析式;
解析式;
(2)若过点![]() 的直线
的直线![]() 平行于直线
平行于直线![]() 且直线
且直线![]() 与二次函数图象只有一个交点
与二次函数图象只有一个交点![]() ,求交点
,求交点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】边长为2的正方形![]() 在平面直角坐标系中的位置如图所示,点
在平面直角坐标系中的位置如图所示,点![]() 是边
是边![]() 的中点,连接
的中点,连接![]() ,点
,点![]() 在第一象限,且
在第一象限,且![]() ,
,![]() .以直线
.以直线![]() 为对称轴的抛物线过
为对称轴的抛物线过![]() ,
,![]() 两点.
两点.

(1)求抛物线的解析式;
(2)点![]() 从点
从点![]() 出发,沿射线
出发,沿射线![]() 每秒1个单位长度的速度运动,运动时间为
每秒1个单位长度的速度运动,运动时间为![]() 秒.过点
秒.过点![]() 作
作![]() 于点
于点![]() ,当
,当![]() 为何值时,以点
为何值时,以点![]() ,
,![]() ,
,![]() 为顶点的三角形与
为顶点的三角形与![]() 相似?
相似?
(3)点![]() 为直线
为直线![]() 上一动点,点
上一动点,点![]() 为抛物线上一动点,是否存在点
为抛物线上一动点,是否存在点![]() ,
,![]() ,使得以点
,使得以点![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形是平行四边形?若存在,请直接写出满足条件的点的坐标;若不存在,请说明理由.
为顶点的四边形是平行四边形?若存在,请直接写出满足条件的点的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com