
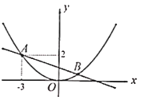
【题目】已知二次函数图象的顶点在原点![]() ,对称轴为
,对称轴为![]() 轴.直线
轴.直线![]() 的图象与二次函数的图象交于点
的图象与二次函数的图象交于点![]() 和点
和点![]() (点
(点![]() 在点
在点![]() 的左侧)
的左侧)
(1)求![]() 的值及直线
的值及直线![]() 解析式;
解析式;
(2)若过点![]() 的直线
的直线![]() 平行于直线
平行于直线![]() 且直线
且直线![]() 与二次函数图象只有一个交点
与二次函数图象只有一个交点![]() ,求交点
,求交点![]() 的坐标.
的坐标.
【答案】(1)m=![]() ,
,![]() ;(2)
;(2)![]()
【解析】
(1)由于抛物线的顶点为原点,因此可设其解析式为y=ax2,直接将A点,B点的坐标代入抛物线中即可求出抛物线的解析式以及m的值,进而可知出点B的坐标,再将A,B点的坐标代入一次函数中,即可求出一次函数的解析式.
(2)根据题意可知直线l2的解析式![]() ,由抛物线与l2只有一个交点,联立直线
,由抛物线与l2只有一个交点,联立直线![]() 与二次函数的解析式,消去y,得出一个含x一元二次方程,根据方程的判别式为0可求得n的值,进而得出结果.
与二次函数的解析式,消去y,得出一个含x一元二次方程,根据方程的判别式为0可求得n的值,进而得出结果.
(1)解:假设二次函数的解析式为![]() ,
,
将![]() 分别代入二次函数的解析式
分别代入二次函数的解析式![]() ,
,
得: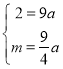 ,解得
,解得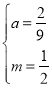 .
.
解得:![]() .
.
![]() 将
将![]() 代入
代入![]() 中,
中,
得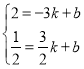 ,,解得:
,,解得: .
.
![]() 的解析式为
的解析式为![]() .
.
(2)由题意可知:l2∥l1,
可设直线![]() 的解析式为:
的解析式为:![]()
![]() 过点
过点![]() ,则有:
,则有:![]() .
.
![]() .
.
由题意,联立直线![]() 与二次函数的解析式,可得以下方程组:
与二次函数的解析式,可得以下方程组:
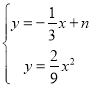 ,
,
消元,得:![]() ,
,
整理,得:![]() , ①
, ①
由题意,得![]() 与
与![]() 只有一个交点,
只有一个交点,
可得:![]() ,
,
解得:![]() .
.
将![]() 代回方程①中,得
代回方程①中,得![]() .
.
将![]() 代入
代入![]() 中,
中,
得![]() .
.
可得交点![]() 坐标为
坐标为![]() .
.


科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,抛物线y=ax2﹣2x﹣3a与x轴交于A、B两点,与y轴交于C点,OC=OB,点P为抛物线上一动点
(1)求抛物线的解析式;
(2)当点P运动到抛物线对称轴右侧时如图2,连PC、BC、BP得△BCP.设△BCP的面积为s,点P的横坐标为x.若s<![]() ,求x的取值范围;
,求x的取值范围;
(3)当点P运动到第四象限时,连AP、BP,BP交y轴于点R,过B作直线l∥AP交y轴于点Q,问:QR、OC之间是否存在确定的数量关系?若存在,请求出并证明;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
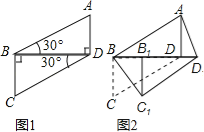
【题目】将两块全等的含30°角的三角尺如图1摆放在一起,设较短直角边为1,如图2,将Rt△BCD沿射线BD方向平移,在平移的过程中,当点B的移动距离为 时,四边ABC1D1为矩形;当点B的移动距离为 时,四边形ABC1D1为菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知BD⊥AB于点B,AC⊥AB于点A,且BD=3,AC=2,AB=m,在线段AB上找一点E,使△BDE与△ACE相似,若这样的点E有且只有两个,则m的值是______
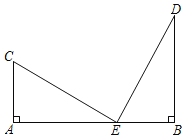
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,以边
,以边![]() 的中点
的中点![]() 为圆心作半圆,使
为圆心作半圆,使![]() 与半圆相切,点
与半圆相切,点![]() 分别是边
分别是边![]() 和半圆上的动点,连接
和半圆上的动点,连接![]() ,则
,则![]() 长的最大值与最小值的和是( )
长的最大值与最小值的和是( )
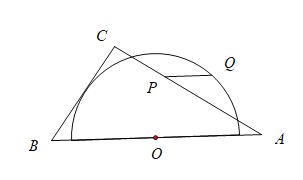
A.8B.9C.10D.12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】九年级(1)班的小华和小红两名学生10次数学测试成绩如下表(表I)所示:
小花 | 70 | 80 | 90 | 80 | 70 | 90 | 80 | 100 | 60 | 80 |
小红 | 90 | 80 | 100 | 60 | 90 | 80 | 90 | 60 | 60 | 90 |
现根据上表数据进行统计得到下表(表Ⅱ):
姓名 | 平均成绩 | 中位数 | 众数 |
小华 | 80 | ||
小红 | 80 | 90 |
(1)填空:根据表I的数据完成表Ⅱ中所缺的数据;
(2)老师计算了小红的方差![]() 请你计算小华的方差并说明哪名学生的成绩较为稳定.
请你计算小华的方差并说明哪名学生的成绩较为稳定.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一艘轮船从位于灯塔C的北偏东60°方向,距离灯塔60 n mile的小岛A出发,沿正南方向航行一段时间后,到达位于灯塔C的南偏东45°方向上的B处,这时轮船B与小岛A的距离是( )

A.![]() n mileB.60 n mileC.120 n mileD.
n mileB.60 n mileC.120 n mileD.![]() n mile
n mile
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某玩具商店以每件60元为成本购进一批新型玩具,以每件100元的价格销售则每天可卖出20件,为了扩大销售,增加盈利,尽快减少库存,商店决定采取适当的降价措施,经调查发现:若每件玩具每降价1元,则每天可多卖2件.
(1)若商店打算每天盈利1200元,每件玩具的售价应定为多少元?
(2)若商店为追求效益最大化,每件玩具的售价定为多少元时,商店每天盈利最多?最多盈利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】手机微信推出了红包游戏,它有多种玩法,其中一种为“拼手气红包”,用户设好总金额以及红包个数后,可以生成不等金额的红包,现有一用户发了三个“拼手气红包”,总金额为3元,随机被甲、乙、丙三人抢到.
(1)下列事件中,确定事件是 ,①丙抢到金额为1元的红包;②乙抢到金额为4元的红包;③甲、乙两人抢到的红包金额之和一定比丙抢到的红包金额多
(2)记金额最多、居中、最少的红包分别为A,B,C.求甲抢到红包A,乙抢到红包C的概率
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com