
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,以边
,以边![]() 的中点
的中点![]() 为圆心作半圆,使
为圆心作半圆,使![]() 与半圆相切,点
与半圆相切,点![]() 分别是边
分别是边![]() 和半圆上的动点,连接
和半圆上的动点,连接![]() ,则
,则![]() 长的最大值与最小值的和是( )
长的最大值与最小值的和是( )
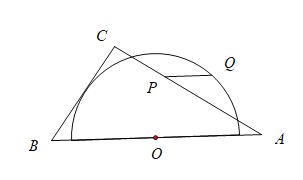
A.8B.9C.10D.12
【答案】C
【解析】
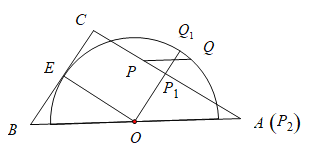
如图,设⊙O与BC相切于点E,连接OE,作OP1⊥AC垂足为P1交⊙O于Q1,此时垂线段OP1最短,P1Q1最小值为OQ1-OP1,如图当Q2在AB边上时,P2与A重合时,P2Q2最大值,由此不难解决问题.
解:如图,设⊙O与BC相切于点E,连接OE,作OP1⊥AC垂足为P1交⊙O于Q1,
此时垂线段OP1最短,P1Q1最小值为OQ1-OP1,
∵AB=10,AC=8,BC=6,
∴AB2=AC2+BC2,∴∠C=90°,
∵∠OP1A=90°,∴OP1∥BC.
∵O为AB的中点,∴P1C=P1A,OP1=![]() BC=3.
BC=3.
又∵BC是⊙O的切线,∴∠OEB=90°,
∴OE∥AC,又O为AB的中点,
∴OE=![]() AC=4=OQ1.
AC=4=OQ1.
∴P1Q1最小值为OQ1-OP1=4-3=1,
如图,当Q2在AB边上时,P2与A重合时,P2Q2经过圆心,经过圆心的弦最长,
P2Q2最大值=AO+OQ2=5+4=9,
∴PQ长的最大值与最小值的和是10.
故选:C.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
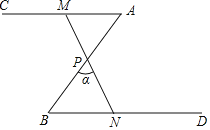
【题目】如图,∠A=∠B=50°,P为AB中点,点M为射线AC上(不与点A重合)的任意点,连接MP,并使MP的延长线交射线BD于点N,设∠BPN=α.
(1)求证:△APM≌△BPN;
(2)当MN=2BN时,求α的度数;
(3)若△BPN的外心在该三角形的内部,直接写出α的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为“节能减排,保护环境”,某村计划建造A、B两种型号的沼气池共20个,以解决所有农户的燃料问题.据市场调查:建造A、B两种型号的沼气池各1个,共需费用5万元;建造A型号的沼气池3个,B种型号的沼气池4个,共需费用18万元.
(1)求建造A、B两种型号的沼气池造价分别是多少?
(2)设建造A型沼气池x个,总费用为y万元,求y与x之间的函数关系式;若要使投入总费用不超过52万元,至少要建造A型沼气池多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为减少环境污染,提高生产效率,公司计划对A、B两类生产线全部进行改造.改造一条A类生产线和两条B类生产线共需资金200万元;改造两条A类生产线和一条B类生产线共需资金175万元.
(1)改造一条A类生产线和一条B类生产线所需的资金分别是多少万元?
(2)公司计划今年对A,B两类生产线共6条进行改造,改造资金由公司自筹和国家财政补贴共同承担.若今年公司自筹的改造资金不超过320万元;国家财政补贴投入的改造资金不少于70万元,其中国家财政补贴投入到A、B两类生产线的改造资金分别为每条10万元和15万元.请你通过计算求出有几种改造方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
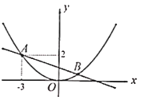
【题目】已知二次函数图象的顶点在原点![]() ,对称轴为
,对称轴为![]() 轴.直线
轴.直线![]() 的图象与二次函数的图象交于点
的图象与二次函数的图象交于点![]() 和点
和点![]() (点
(点![]() 在点
在点![]() 的左侧)
的左侧)
(1)求![]() 的值及直线
的值及直线![]() 解析式;
解析式;
(2)若过点![]() 的直线
的直线![]() 平行于直线
平行于直线![]() 且直线
且直线![]() 与二次函数图象只有一个交点
与二次函数图象只有一个交点![]() ,求交点
,求交点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
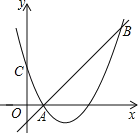
【题目】如图,二次函数y=(x﹣2)2+m的图象与y轴交于点C,点B是点C关于该二次函数图象的对称轴对称的点.已知一次函数y=kx+b的图象经过该二次函数图象上点A(1,0)及点B.
(1)求二次函数与一次函数的解析式;
(2)根据图象,写出满足kx+b≥(x﹣2)2+m的x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知抛物线
中,已知抛物线![]() .
.
(1)当![]() 时,
时,
①抛物线![]() 的对称轴为
的对称轴为![]() ________;
________;
②若在抛物线![]() 上有两点
上有两点![]() ,且
,且![]() ,则
,则![]() 的取值范围是________;
的取值范围是________;
(2)抛物线![]() 的对称轴与
的对称轴与![]() 轴交于点
轴交于点![]() ,点
,点![]() 与点
与点![]() 关于
关于![]() 轴对称,将点
轴对称,将点![]() 向右平移3个单位得到点
向右平移3个单位得到点![]() ,若抛物线
,若抛物线![]() 与线段
与线段![]() 恰有一个公共点,结合图象,求
恰有一个公共点,结合图象,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
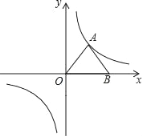
【题目】如图,在反比例函数图象中,△AOB是等边三角形,点A在双曲线的一支上,将△AOB绕点O顺时针旋转α (0°<α<360° ),使点A仍在双曲线上,则α=_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com