
【题目】为减少环境污染,提高生产效率,公司计划对A、B两类生产线全部进行改造.改造一条A类生产线和两条B类生产线共需资金200万元;改造两条A类生产线和一条B类生产线共需资金175万元.
(1)改造一条A类生产线和一条B类生产线所需的资金分别是多少万元?
(2)公司计划今年对A,B两类生产线共6条进行改造,改造资金由公司自筹和国家财政补贴共同承担.若今年公司自筹的改造资金不超过320万元;国家财政补贴投入的改造资金不少于70万元,其中国家财政补贴投入到A、B两类生产线的改造资金分别为每条10万元和15万元.请你通过计算求出有几种改造方案?
【答案】(1)改造一条A类生产线需要资金50万元,改造一条B类生产线需要资金75万元;(2)共有3种改造方案.
【解析】
(1)设改造一条A类生产线需要资金x万元,改造一条B类生产线需要资金y万元,根据“改造一条A类生产线和两条B类生产线共需资金200万元;改造两条A类生产线和一条B类生产线共需资金175万元”,即可得出关于x,y的二元一次方程组,解之即可得出结论;
(2)设改造m条A类生产线,则改造(6﹣m)条B类生产线,根据该公司自筹的改造资金不超过320万元且国家财政补贴投入的改造资金不少于70万元,即可得出关于m的一元一次不等式组,解之即可得出m的取值范围,再结合m为整数即可得出改造方案的数量.
解:(1)设改造一条A类生产线需要资金x万元,改造一条B类生产线需要资金y万元,
依题意,得:![]() ,
,
解得:![]() .
.
答:改造一条A类生产线需要资金50万元,改造一条B类生产线需要资金75万元.
(2)设改造m条A类生产线,则改造(6﹣m)条B类生产线,
依题意,得: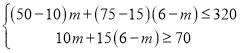 ,
,
解得:2≤m≤4.
∵m为正整数,
∴m=2,3,4.
答:共有3种改造方案.


科目:初中数学 来源: 题型:
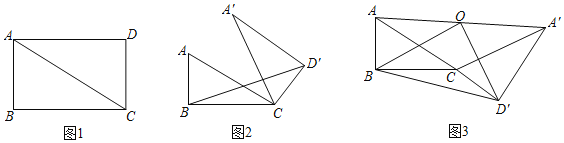
【题目】如图1,矩形ABCD中,∠ACB=30°,将△ACD绕C点顺时针旋转α(0°<α<360°)至△A'CD'位置.
(1)如图2,若AB=2,α=30°,求S△BCD′.
(2)如图3,取AA′中点O,连OB、OD′、BD′.若△OBD′存在,试判定△OBD′的形状.
(3)当α=α1时,OB=OD′,则α1= °;当α=α2时,△OBD′不存在,则α2= °.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 是直径AB所对的半圆弧,点C在
是直径AB所对的半圆弧,点C在![]() 上,且∠CAB =30°,D为AB边上的动点(点D与点B不重合),连接CD,过点D作DE⊥CD交直线AC于点E.
上,且∠CAB =30°,D为AB边上的动点(点D与点B不重合),连接CD,过点D作DE⊥CD交直线AC于点E.
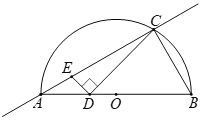
小明根据学习函数的经验,对线段AE,AD长度之间的关系进行了探究.
下面是小明的探究过程,请补充完整:
(1)对于点D在AB上的不同位置,画图、测量,得到线段AE,AD长度的几组值,如下表:
位置1 | 位置2 | 位置3 | 位置4 | 位置5 | 位置6 | 位置7 | 位置8 | 位置9 | ||
AE/cm | 0.00 | 0.41 | 0.77 | 1.00 | 1.15 | 1.00 | 0.00 | 1.00 | 4.04 | … |
AD/cm | 0.00 | 0.50 | 1.00 | 1.41 | 2.00 | 2.45 | td style="width:10%; border-top-style:solid; border-top-width:0.75pt; border-right-style:solid; border-right-width:0.75pt; border-left-style:solid; border-left-width:0.75pt; padding:3.38pt 5.03pt; vertical-align:middle">3.21 | 3.50 | … |
在AE,AD的长度这两个量中,确定_______的长度是自变量,________的长度是这个自变量的函数;
(2)在下面的平面直角坐标系![]() 中,画出(1)中所确定的函数的图象;
中,画出(1)中所确定的函数的图象;
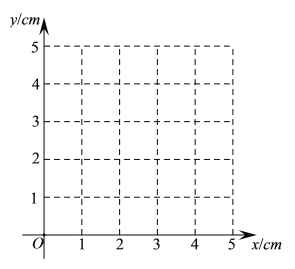
(3)结合画出的函数图象,解决问题:当AE=![]() AD时,AD的长度约为________cm(结果精确到0.1).
AD时,AD的长度约为________cm(结果精确到0.1).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边△ABC中,D,E,F分别是BC,AC,AB上的点,DE⊥AC,EF⊥AB,
FD⊥BC,则△DEF的面积与△ABC的面积之比等于( )

A.1∶3 B.2∶3 C.![]() ∶2 D.
∶2 D.![]() ∶3
∶3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某种进价为每件40元的商品,通过调查发现,当销售单价在40元至65元之间(![]() )时,每月的销售量
)时,每月的销售量![]() (件)与销售单价
(件)与销售单价![]() (元)之间满足如图所示的一次函数关系.
(元)之间满足如图所示的一次函数关系.
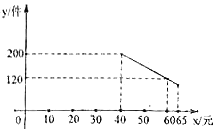
(1)求![]() 与
与![]() 的函数关系式;
的函数关系式;
(2)设每月获得的利润为![]() (元),求
(元),求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(3)若想每月获得1600元的利润,那么销售单价应定为多少元?
(4)当销售单价定为多少元时,每月的销售利润最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,以边
,以边![]() 的中点
的中点![]() 为圆心作半圆,使
为圆心作半圆,使![]() 与半圆相切,点
与半圆相切,点![]() 分别是边
分别是边![]() 和半圆上的动点,连接
和半圆上的动点,连接![]() ,则
,则![]() 长的最大值与最小值的和是( )
长的最大值与最小值的和是( )
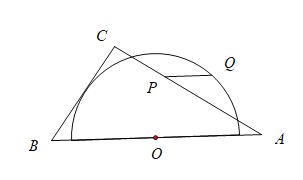
A.8B.9C.10D.12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某数学活动小组为测量学校旗杆AB的高度,沿旗杆正前方![]() 米处的点C出发,沿斜面坡度
米处的点C出发,沿斜面坡度![]() 的斜坡CD前进4米到达点D,在点D处安置测角仪,测得旗杆顶部A的仰角为37°,量得仪器的高DE为1.5米.已知A、B、C、D、E在同一平面内,AB⊥BC,AB//DE.求旗杆AB的高度.(参考数据:sin37°≈
的斜坡CD前进4米到达点D,在点D处安置测角仪,测得旗杆顶部A的仰角为37°,量得仪器的高DE为1.5米.已知A、B、C、D、E在同一平面内,AB⊥BC,AB//DE.求旗杆AB的高度.(参考数据:sin37°≈![]() ,cos37°≈
,cos37°≈![]() ,tan37°≈
,tan37°≈![]() .计算结果保留根号)
.计算结果保留根号)

查看答案和解析>>
科目:初中数学 来源: 题型:
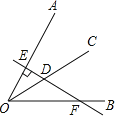
【题目】已知∠AOB=60°,OC是∠AOB的平分线,点D为OC上一点,过D作直线DE⊥OA,垂足为点E,且直线DE交OB于点F,如图所示.若DE=2,则DF=_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com