
【题目】已知抛物线的解析式y=ax2+bx+3与x轴交于A、B两点,点B的坐标为(﹣1,0)抛物线与y轴正半轴交于点C,△ABC面积为6.
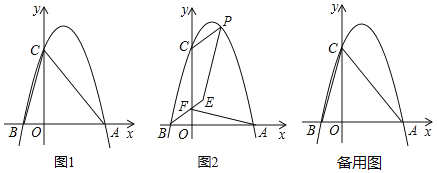
(1)如图1,求此抛物线的解析式;
(2)P为第一象限抛物线上一动点,过P作PG⊥AC,垂足为点G,设点P的横坐标为t,线段PG的长为d,求d与t之间的函数关系式,并直接写出自变量t的取值范围;
(3)如图2,在(2)的条件下,过点B作CP的平行线交y轴上一点F,连接AF,在BF的延长线上取点E,连接PE,若PE=AF,∠AFE+∠BEP=180°,求点P的坐标.
【答案】(1)y=﹣x2+2x+3;(2)![]() ,0<t<3;(3)P(
,0<t<3;(3)P(![]() )
)
【解析】
(1)根据条件易求出A,B两点的坐标,再利用待定系数法求解即可;
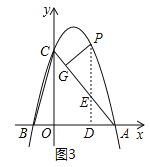
(2)作PD⊥x轴交AC于点E,如图3,易知∠A=45°,然后利用三角形的内角和可得:∠P=∠A,则![]() ,再利用待定系数法求出直线AC的解析式,而点P的横坐标已知,则可用含t的代数式表示出PE,问题即得解决;
,再利用待定系数法求出直线AC的解析式,而点P的横坐标已知,则可用含t的代数式表示出PE,问题即得解决;
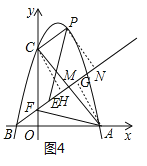
(3)如图4,过点P作PN⊥BE交BE于点N,过点C作CH⊥BE于点H,过点A作AG⊥BE于点G,设BE与AC交于点M,根据AAS可证明△PEN≌△AFG,可得PN=AG,然后再根据AAS证明△CHM≌△AGM,可得CM=AM,于是由中点坐标公式可求得点M的坐标,再根据待定系数法可求得直线BM的解析式,进而求出直线CP的解析式,然后解由直线CP和抛物线的解析式组成的方程组即可求出点P的坐标.
解:(1)当x=0时,y=3,∴C(0,3),∴OC=3,
∵B(﹣1,0),∴OB=1,∴![]() ,解得:AB=4,
,解得:AB=4,
∴OA=AB﹣OB=3,∴A(3,0),
将A,B的坐标代入抛物线的解析式y=ax2+bx+3,得:![]() ,解得;
,解得;![]() ,
,
∴抛物线的解析式为y=﹣x2+2x+3;
(2)作PD⊥x轴交AC于点E,如图3,
∵OA=OC=3,∴∠A=45°,
∵∠PEG=∠AED,∠PGE=∠EDA=90°,∴∠P=∠A=45°,
∴![]() ,∴
,∴![]() ,
,
设直线AC的解析式为:y=kx+b,把A(3,0),C(0,3)两点代入,得:![]() ,解得:
,解得:![]() ,
,
∴直线AC为y=﹣x+3,
设P(t,﹣t2+2t+3),∵PD⊥x轴,∴E(t,﹣t+3),
∴PE=﹣t2+2t+3+t﹣3=﹣t2+3t,∴![]() ,
,
∵P为第一象限抛物线上一动点,∴0<t<3;
∴![]() ,0<t<3;
,0<t<3;
(3)如图4,过点P作PN⊥BE交BE于点N,过点C作CH⊥BE于点H,过点A作AG⊥BE于点G,设BE与AC交于点M,
∵∠BEP+∠PEN=180°,∠AFE+∠BEP=180°,∴∠PEN=∠AFG,
∵∠PNE=∠AGF=90°,PE=AF,
∴△PEN≌△AFG(AAS),∴PN=AG,
∵CP∥BE,∴四边形CPNH是矩形,∴PN=CH=AG,
∵∠CMH=∠AMG,∠CHM=∠AGM,
∴△CHM≌△AGM(AAS),∴CM=AM,∴M(![]() ,
,![]() ),
),
则可得过点B(-1,0)和点M(![]() ,
,![]() )两点的直线解析式为:y=
)两点的直线解析式为:y=![]() ,
,
∵CP∥BM,∴直线CP的解析式为y=![]() ,
,
解方程组: ,得:
,得:![]() ,
,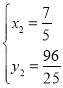 ,
,
∴P(![]() ).
).


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 的图与y轴分别交于点A,且反比例函数
的图与y轴分别交于点A,且反比例函数![]() 的图象在第一象限内的交点为M.
的图象在第一象限内的交点为M.
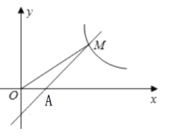
(1)求点M的坐标.
(2)在x轴上是否存在点P,使AM⊥MP?若存在,求出点P的坐标;若不存在,说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=2x﹣4分别交坐标轴于A、B两点,交双曲线y=![]() (x>0)于C点,且sin∠COB=
(x>0)于C点,且sin∠COB=![]() ;
;
(1)求双曲线的解析式;
(2)若过点B的直线y=ax+b(a>0)交y轴于D点,交双曲线于点E,且OD:AD=1:2,求E点横坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在网格纸中,![]() 、
、![]() 都是格点,以
都是格点,以![]() 为圆心,
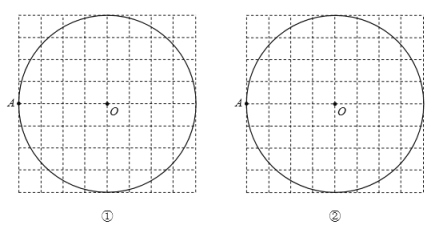
为圆心,![]() 为半径作圆,用无刻度的直尺完成以下画图:(不写画法)
为半径作圆,用无刻度的直尺完成以下画图:(不写画法)
(1)在圆①中画圆![]() 的一个内接正六边形
的一个内接正六边形![]() ;
;
(2)在图②中画圆![]() 的一个内接正八边形
的一个内接正八边形![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
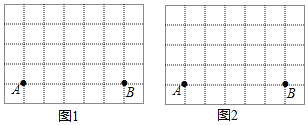
【题目】如图是两张形状,大小完全相同的方格纸,方格纸中的每个小正方形的边长均为1,点A,B均在小正方形的顶点上.
(1)在图1中画出面积为5的△ABC,且△ABC中有一个角为45°;
(2)在图2中画出△ABD,且∠ADB=90°并直接写出△ABD的周长.(C,D都在方格顶点上,每幅图画出一种情况即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
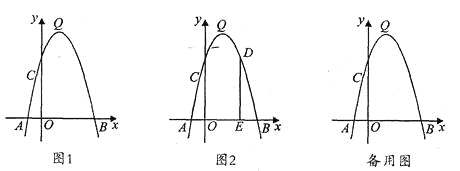
【题目】如图1,抛物线y=-x2+bx+c的顶点为Q,与x轴交于A(-1,0)、B(5,0)两点,与y轴交于点C.
(1)求抛物线的解析式及其顶点Q的坐标;
(2)在该抛物线的对称轴上求一点P,使得△PAC的周长最小,请在图中画出点P的位置,并求点P的坐标;
(3)如图2,若点D是第一象限抛物线上的一个动点,过D作DE⊥x轴,垂足为E.
①有一个同学说:“在第一象限抛物线上的所有点中,抛物线的顶点Q与x轴相距最远,所以当点D运动至点Q时,折线D-E-O的长度最长”,这个同学的说法正确吗?请说明理由.
②若DE与直线BC交于点F.试探究:四边形DCEB能否为平行四边形?若能,请直接写出点D的坐标;若不能,请简要说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
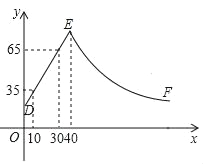
【题目】某化工车间发生有害气体泄漏,自泄漏开始到完全控制利用了40min,之后将对泄漏有害气体进行清理,线段DE表示气体泄漏时车间内危险检测表显示数据y与时间x(min)之间的函数关系(0≤x≤40),反比例函数y=![]() 对应曲线EF表示气体泄漏控制之后车间危险检测表显示数据y与时间x(min)之间的函数关系(40≤x≤?).根据图象解答下列问题:
对应曲线EF表示气体泄漏控制之后车间危险检测表显示数据y与时间x(min)之间的函数关系(40≤x≤?).根据图象解答下列问题:
(1)危险检测表在气体泄漏之初显示的数据是 ;
(2)求反比例函数y=![]() 的表达式,并确定车间内危险检测表恢复到气体泄漏之初数据时对应x的值.
的表达式,并确定车间内危险检测表恢复到气体泄漏之初数据时对应x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
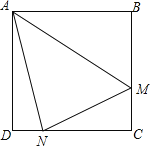
【题目】如图,在正方形![]() 中,点
中,点![]() 、
、![]() 为边
为边![]() 和
和![]() 上的动点(不含端点),
上的动点(不含端点),![]() .下列三个结论:①当
.下列三个结论:①当![]() 时,则
时,则![]() ;②
;②![]() ;③
;③![]() 的周长不变,其中正确结论的个数是( )
的周长不变,其中正确结论的个数是( )
A.0B.1
C.2D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是小华同学设计的“作三角形的高线”的尺规作图的过程.
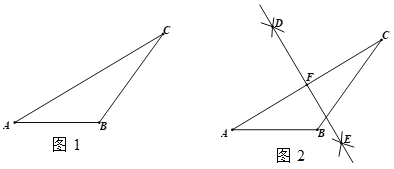
已知:如图1,△ABC.
求作:AB边上的高线.
作法:如图2,
①分别以A,C为圆心,大于![]() 长
长
为半径作弧,两弧分别交于点D,E;
② 作直线DE,交AC于点F;
③ 以点F为圆心,FA长为半径作圆,交AB的延长线于点M;
④ 连接CM.
则CM 为所求AB边上的高线.
根据上述作图过程,回答问题:
(1)用直尺和圆规,补全图2中的图形;
(2)完成下面的证明:
证明:连接DA,DC,EA,EC,
∵由作图可知DA=DC =EA=EC,
∴DE是线段AC的垂直平分线.
∴FA=FC .
∴AC是⊙F的直径.
∴∠AMC=______°(___________________________________)(填依据),
∴CM⊥AB.
即CM就是AB边上的高线.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com