
【题目】如图,在正方形![]() 中,点
中,点![]() 、
、![]() 为边
为边![]() 和
和![]() 上的动点(不含端点),
上的动点(不含端点),![]() .下列三个结论:①当
.下列三个结论:①当![]() 时,则
时,则![]() ;②
;②![]() ;③
;③![]() 的周长不变,其中正确结论的个数是( )
的周长不变,其中正确结论的个数是( )
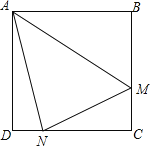
A.0B.1
C.2D.3
【答案】D
【解析】
根据题目条件判定△AND≌△AMB,从而判断①的正误;利用截长补短的方法判定三角形全等,从而判断②③正误.
解:在正方形ABCD中,AD=AB=CD=CB,∠D=∠B=∠C=90°
∵![]()
∴![]()
∴∠NMC=45°,△MNC是等腰直角三角形
∴NC=MC
∴DN=BM
所以△AND≌△AMB
∴![]() ,因此①正确;
,因此①正确;
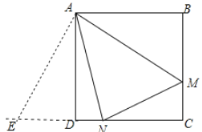
如图:延长CD,使得DE=BM
在△ADE和△ABM中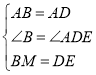
∴△ADE≌△ABM
∴![]() ,AM=AE
,AM=AE
∵![]()
∴![]()
∴![]()
∴![]()
又∵AE=AM,AN=AN
∴△AEN≌△AMN
∴MN=EN=ED+DN=BM+DN
∠AMN=∠E,∠ANM=∠ANE
∴∠ENM=∠ANM+∠ANE=2(180°-45°-∠AMN)=270°-2∠AMN
而∠MNC=180°-∠ENM=180°-(270°-2∠AMN)=2∠AMN-90°
即②![]() ,正确;
,正确;
![]() 的周长=MN+MC+NC=EN+NC+MC=ED+DN+NC+MC=BM+DN+NC+MC=CD+BC,即正方形边长的2倍,∴③
的周长=MN+MC+NC=EN+NC+MC=ED+DN+NC+MC=BM+DN+NC+MC=CD+BC,即正方形边长的2倍,∴③![]() 的周长不变,正确
的周长不变,正确
正确的共三个,故选:D.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,∠BCD=90°,且BC=DC,直线PQ经过点D.设∠PDC=α(45°<α<135°),BA⊥PQ于点A,将射线CA绕点C按逆时针方向旋转90°,与直线PQ交于点E.
(1)当α=125°时,∠ABC= °;
(2)求证:AC=CE;
(3)若△ABC的外心在其内部,直接写出α的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线的解析式y=ax2+bx+3与x轴交于A、B两点,点B的坐标为(﹣1,0)抛物线与y轴正半轴交于点C,△ABC面积为6.
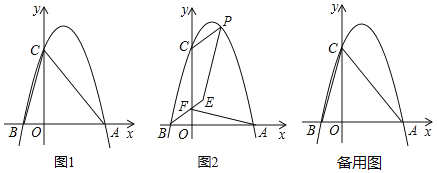
(1)如图1,求此抛物线的解析式;
(2)P为第一象限抛物线上一动点,过P作PG⊥AC,垂足为点G,设点P的横坐标为t,线段PG的长为d,求d与t之间的函数关系式,并直接写出自变量t的取值范围;
(3)如图2,在(2)的条件下,过点B作CP的平行线交y轴上一点F,连接AF,在BF的延长线上取点E,连接PE,若PE=AF,∠AFE+∠BEP=180°,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)(教材呈现)下图是华师版九年级上册数学教材第77页的部分内容.请根据教材提示,结合图23.4.2,写出完整的证明过程.

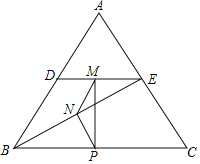
(2)(结论应用)如图,△ABC是等边三角形,点D在边AB上(点D与点A、B不重合),过点D作DE∥BC交AC于点E,连结BE,M、N、P分别为DE、BE、BC的中点,顺次连结M、N、P.
①求证:MN=PN;
②∠MNP的大小是.
查看答案和解析>>
科目:初中数学 来源: 题型:
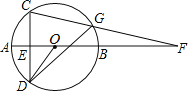
【题目】如图,AB是⊙O的直径,弦CD⊥AB于点E,点G为弧BC上一动点,CG与AB的延长线交于点F,连接OD.
(1)判定∠AOD与∠CGD的大小关系为 ,并求证:GB平分∠DGF.
(2)在G点运动过程中,当GD=GF时,DE=4,BF=![]() ,求⊙O的半径.
,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
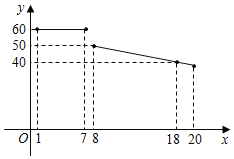
【题目】某水果超市经销一种进价为18元/kg的水果,根据以前的销售经验,该种水果的最佳销售期为20天,销售人员整理出这种水果的销售单价y(元/kg)与第x天(1≤x≤20)的函数图象如图所示,而第x天(1≤x≤20)的销售量m(kg)是x的一次函数,满足下表:
x(天) | 1 | 2 | 3 | … |
m(kg) | 20 | 24 | 28 | … |
(1)请分别写出销售单价y(元/kg)与x(天)之间及销售量m(kg)是x(天)的之间的函数关系式
(2)求在销售的第几天时,当天的利润最大,最大利润是多少?
(3)请求出试销的20天中当天的销售利润不低于1680元的天数.
查看答案和解析>>
科目:初中数学 来源: 题型:
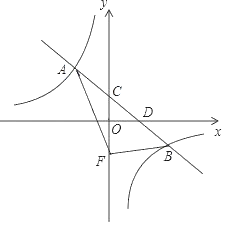
【题目】在平面直角坐标系中,一次函数y=﹣![]() x+b的图象与反比例函数y=
x+b的图象与反比例函数y=![]() (k≠0)图象交于A、B两点,与y轴交于点C,与x轴交于点D,其中A点坐标为(﹣2,3).
(k≠0)图象交于A、B两点,与y轴交于点C,与x轴交于点D,其中A点坐标为(﹣2,3).
(1)求一次函数和反比例函数解析式.
(2)若将点C沿y轴向下平移4个单位长度至点F,连接AF、BF,求△ABF的面积.
(3)根据图象,直接写出不等式﹣![]() x+b>
x+b>![]() 的解集.
的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
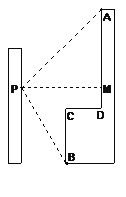
【题目】小强在教学楼的点P处观察对面的办公大楼.为了测量点P到对面办公大楼上部AD的距离,小强测得办公大楼顶部点A的仰角为45°,测得办公大楼底部点B的俯角为60°,已知办公大楼高46米,CD=10米.求点P到AD的距离(用含根号的式子表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,D、E分别是边AC、BC的中点,F是BC延长线上一点,∠F=∠B.

(l)若AB=1O,求FD的长;
(2)若AC=BC.求证:△CDE∽△DFE .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com