
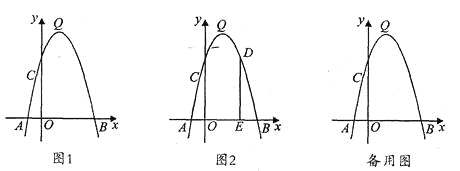
����Ŀ����ͼ1��������y=��x2��bx��c�Ķ���ΪQ����x�ύ��A����1��0����B(5��0)���㣬��y�ύ�ڵ�C��
(1)�������ߵĽ���ʽ���䶥��Q�����ꣻ
(2)�ڸ������ߵĶԳ�������һ��P��ʹ����PAC���ܳ���С������ͼ�л�����P��λ�ã������P�����ꣻ
(3)��ͼ2������D�ǵ�һ�����������ϵ�һ�����㣬��D��DE��x�ᣬ����ΪE��
����һ��ͬѧ˵�����ڵ�һ�����������ϵ����е��У������ߵĶ���Q��x�������Զ�����Ե���D�˶�����Qʱ������D��E��O�ij�����������ͬѧ��˵����ȷ����˵�����ɣ�
����DE��ֱ��BC���ڵ�F����̽�����ı���DCEB�ܷ�Ϊƽ���ı��Σ����ܣ���ֱ��д����D�����ꣻ�����ܣ����Ҫ˵�����ɣ�
���𰸡���1��y-��x-2��2+9��Q��2��9������2����2��3������ͼ����������3���ٲ���ȷ�����ɼ��������ڲ��ܣ����ɼ�����.
��������
��1����A��-1��0����B��5��0���ֱ����y=-x2+bx+c�м���ȷ��b��c��ֵ��Ȼ���䷽��ȷ���䶥�����ꣻ
��2������BC�����Գ����ڵ�P������AP��AC�����C��������Ȼ��ȷ��ֱ��BC�Ľ���ʽ������������x=2��ֱ��BC�Ľ������꼴Ϊ��P�����ꣻ
��3������D��t��-t2+4t+5����������D-E-O�ij���ΪL�����L�����ֵ���뵱��D��Q�غ�ʱL=9+2=11��![]() ��Ƚϼ��ɵõ��𰸣�
��Ƚϼ��ɵõ��𰸣�
�������ı���DCEBΪƽ���ı��Σ���ɵõ�EF=DF��CF=BF��Ȼ�����DE��y�����DF���õ�DF��EF������EF=DF��ì�ܣ��Ӷ�����ƽ���ı��Σ�
��:��1����A��-1��0����B��5��0���ֱ����y=-x2+bx+c�У���
![]() �����
�����![]()
��y=-x2+4x+5��
��y=-x2+4x+5=-��x-2��2+9��
��Q��2��9����
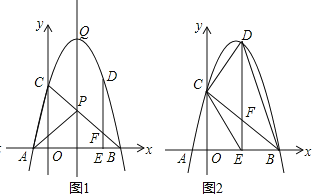
��2����ͼ1������BC�����Գ����ڵ�P������AP��AC��
��AC��Ϊ��ֵ����Ҫʹ��PAC���ܳ���С��ֻ��PA+PC��С��
����A���ڶԳ���x=2�ĶԳƵ��ǵ�B��5��0����������y=-x2+4x+5��y�ύ��C������Ϊ��0��5����
���ɼ���֪ʶ��֪��PA+PC=PB+PCΪ��С��
��ֱ��BC�Ľ���ʽΪy=kx+5����B��5��0������5k+5=0����k=-1��
��y=-x+5��
����x=2ʱ��y=3��
����P��������2��3����
��3�������ͬѧ��˵������ȷ��
����D��t��-t2+4t+5����������D-E-O�ij���ΪL����L=t2+4t+5+t=t2+5t+5=(t![]() )2+
)2+![]() ��
��
��a��0��
����t=![]() ʱ��L���ֵ=
ʱ��L���ֵ=![]() ��
��
������D��Q�غ�ʱ��L=9+2=11��![]() ��
��
���ø�ͬѧ��˵������ȷ��
���ı���DCEB����Ϊƽ���ı��Σ�
��ͼ2�����ı���DCEBΪƽ���ı��Σ���EF=DF��CF=BF��
��DE��y�ᣬ
��![]() ����OE=BE=2.5��
����OE=BE=2.5��
��xF=2.5ʱ��yF=-2.5+5=2.5����EF=2.5��
��xD=2.5ʱ��yD=(2.52)2+9=8.75����DE=8.75��
��DF=DE-EF=8.75-2.5=6.25��2.5����DF��EF������EF=DF��ì�ܣ�
���ı���DCEB����Ϊƽ���ı��Σ�


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ��ѧ�ۺ�ʵ��С���ͬѧ�ԡ���ɫ���С�Ϊ���⣬��ijС���ľ���Թ����������˽��ʹ������������ʾ�����.����ε����У�������20�˶��ڹ����������˽⣬ʹ�ù��������ľ���ÿ������·�̲�����8ǧ�ף�����������������ͳ��ͼ������ͼ��ʾ��
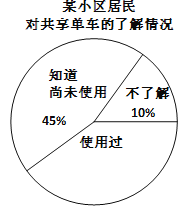
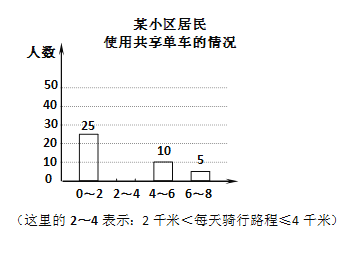
��1�����ε��������� �ˣ�ʹ�ù������������� �ˣ�
��2���뽫����ͳ��ͼ����������
��3��������С����Լ��3000������������ÿ�������·����2��4ǧ���ж����ˣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��l��x�ᣬy��ֱ���A��B���㣬���뷴��������y��![]() ��x��0����ͼ���ڵ�C����S��AOB��S��BOC��1����k����������
��x��0����ͼ���ڵ�C����S��AOB��S��BOC��1����k����������
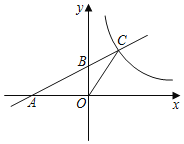
A. 1B. 2C. 3D. 4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ABCD�У���AB��4��BC��2����EΪCD���е㣬FΪAB��һ�㣬����EF��DF��EF��![]() ����DF��_____��
����DF��_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�����ߵĽ���ʽy��ax2+bx+3��x�ύ��A��B���㣬��B������Ϊ����1��0����������y�������ύ�ڵ�C����ABC���Ϊ6��
��1����ͼ1����������ߵĽ���ʽ��
��2��PΪ��һ������������һ���㣬��P��PG��AC������Ϊ��G�����P�ĺ�����Ϊt���߶�PG�ij�Ϊd����d��t֮��ĺ�����ϵʽ����ֱ��д���Ա���t��ȡֵ��Χ��
��3����ͼ2���ڣ�2���������£�����B��CP��ƽ���߽�y����һ��F������AF����BF���ӳ�����ȡ��E������PE����PE��AF����AFE+��BEP��180�������P�����꣮
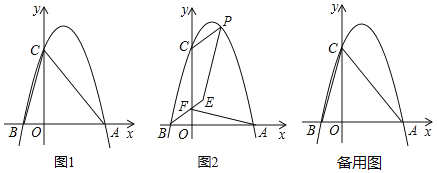
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������![]() ��
��![]() �dz�����������
�dz�����������![]() ��
��
��![]() ����������ߵĽ���ʽ�Ͷ������꣮
����������ߵĽ���ʽ�Ͷ������꣮
��![]() ����������
����������![]() ����һ����Ϊ��
����һ����Ϊ��![]() ����
����![]() �ύ�ڵ�
�ύ�ڵ�![]() ��ƽ����
��ƽ����![]() ���ֱ��
���ֱ��![]() �������߽��ڵ�
�������߽��ڵ�![]() ��
�� ![]() ����ֱ��
����ֱ��![]() ���ڵ�
���ڵ�![]() ��
��
����ֱ��![]() �Ľ���ʽ��
�Ľ���ʽ��
����![]() ����Ϻ�����ͼ����
����Ϻ�����ͼ����![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1�����̲ij��֣���ͼ�ǻ�ʦ����꼶�ϲ���ѧ�̲ĵ�77ҳ�IJ������ݣ�����ݽ̲���ʾ�����ͼ23.4.2��д��������֤�����̣�

��2��������Ӧ�ã���ͼ����ABC�ǵȱ������Σ���D�ڱ�AB�ϣ���D���A��B���غϣ�������D��DE��BC��AC�ڵ�E������BE��M��N��P�ֱ�ΪDE��BE��BC���е㣬˳������M��N��P��
����֤��MN��PN��
�ڡ�MNP�Ĵ�С�ǣ�
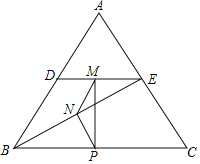
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijˮ�����о���һ�ֽ���Ϊ18Ԫ/kg��ˮ����������ǰ�����۾��飬����ˮ�������������Ϊ20�죬������Ա����������ˮ�������۵���y��Ԫ/kg�����x�죨1��x��20���ĺ���ͼ����ͼ��ʾ������x�죨1��x��20����������m��kg����x��һ�κ����������±���
x���죩 | 1 | 2 | 3 | �� |
m��kg�� | 20 | 24 | 28 | �� |
��1����ֱ�д�����۵���y��Ԫ/kg����x���죩֮�估������m��kg����x���죩��֮��ĺ�����ϵʽ
��2���������۵ĵڼ���ʱ����������������������Ƕ��٣�
��3�������������20���е��������������1680Ԫ��������
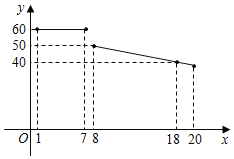
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ij�д�����չ��ɫ��ͨ��������������ɫ��ͨ��ϵ����������������½���������˿������ϴ�ĵط�������ͬѧ������������������������������������������õ����ݷֳ����࣬![]() ������ʹ�ã�
������ʹ�ã�![]() ��ż��ʹ�ã�
��ż��ʹ�ã�![]() ���˽��ʹ�ã�
���˽��ʹ�ã�![]() �����˽⣬������������������������ͳ��ͼ.�����������Ϣ������������⣺
�����˽⣬������������������������ͳ��ͼ.�����������Ϣ������������⣺
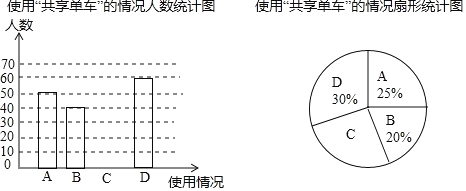
��1����α�������������� �ˣ���![]() ���˽��ʹ������������ �ˣ���
���˽��ʹ������������ �ˣ���![]() �����˽�����ռ����ͳ��ͼ��Բ�ĽǶ���Ϊ .
�����˽�����ռ����ͳ��ͼ��Բ�ĽǶ���Ϊ .
��2��ijС������![]() �ˣ����ݵ�����������ʹ�ù��������������Ĵ�Լ�ж����ˣ�
�ˣ����ݵ�����������ʹ�ù��������������Ĵ�Լ�ж����ˣ�
��3��Ŀǰ�������������л�ɫ����ɫ����ɫ���ֿ�ѡ��ij��С�ź�С��һ��ʹ�����������������У���������ͬһ����ɫ�����ĸ���.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com