
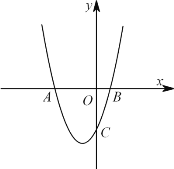
【题目】如图,抛物线![]() 与
与![]() 轴交于
轴交于![]() 、
、![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() .
.
(1)求点![]() 、
、![]() 、
、![]() 的坐标;
的坐标;
(2)若点![]() 在
在![]() 轴的上方,以
轴的上方,以![]() 、
、![]() 、
、![]() 为顶点的三角形与
为顶点的三角形与![]() 全等,平移这条抛物线,使平移后的抛物线经过点
全等,平移这条抛物线,使平移后的抛物线经过点![]() 与点
与点![]() ,请你写出平移过程,并说明理由。
,请你写出平移过程,并说明理由。
【答案】(1)![]() ,
,![]() ,
,![]() ;(2)
;(2)![]() ,
,![]() .理由见解析.
.理由见解析.
【解析】
(1)令![]() 中y=0,求出点A、B的坐标,令x=0即可求出点C的坐标;
中y=0,求出点A、B的坐标,令x=0即可求出点C的坐标;
(2)分两种全等情况求出点D的坐标,再设平移后的解析式,将点B、D的坐标代入即可求出解析式,由平移前的解析式根据顶点式的数值变化得到平移的方向与距离.
(1)令![]() 中y=0,得
中y=0,得![]() ,
,
解得: ![]() ,
,
∴![]() ,
,![]() .
.
当![]() 中x=0时,y=-3,
中x=0时,y=-3,
∴![]() .
.
(2)当△ABD1≌△ABC时,
∵![]() ,
,
∴由轴对称得D1(0,3),
设平移后的函数解析式为![]() ,将点B、D1的坐标代入,得
,将点B、D1的坐标代入,得
![]() ,解得
,解得![]() ,
,
∴平移后的解析式为![]() ,
,
∵平移前的解析式为![]() ,
,
∴将![]() 向右平移3个单位,再向上3个单位得到
向右平移3个单位,再向上3个单位得到![]() ;
;
当△ABD2≌△BAC时,即△ABD2≌△BAD1,
作D2H⊥AB,
∴AH=OB=1,D2H=OD1=3,
∴OH=OA-AH=3-1=2,
∴D2(-2,3),
设平移后的解析式为![]() ,将点B、D2的坐标代入得
,将点B、D2的坐标代入得
![]() ,解得
,解得![]() ,
,
∴平移后的函数解析式为![]() ,
,
∵平移前的解析式为![]() ,
,
∴将![]() 向右平移1个单位,再向上平移3个单位得到
向右平移1个单位,再向上平移3个单位得到![]() .
.


科目:初中数学 来源: 题型:
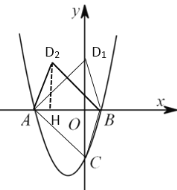
【题目】如图,抛物线y=ax2+bx+3经过点 B(﹣1,0),C(2,3),抛物线与y轴的焦点A,与x轴的另一个焦点为D,点M为线段AD上的一动点,设点M的横坐标为t.
(1)求抛物线的表达式;
(2)过点M作y轴的平行线,交抛物线于点P,设线段PM的长为1,当t为何值时,1的长最大,并求最大值;(先根据题目画图,再计算)
(3)在(2)的条件下,当t为何值时,△PAD的面积最大?并求最大值;
(4)在(2)的条件下,是否存在点P,使△PAD为直角三角形?若存在,直接写出t的值;若不存在,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:若在一个两位正整数N的个位数字与十位数字之间添上数字6,组成一个新的三位数,我们称这个三位数为N的“至善数”,如34的“至善数为364”;若将一个两位正整数M加6后得到一个新数,我们称这个新数为M的“明德数”,如34的“明德数为40”.
(1)30的“至善数”是 ,“明德数”是 .
(2)求证:对任意一个两位正整数A,其“至善数”与“明德数”之差能被9整除;
(3)若一个两位正整数B的明德数的各位数字之和是B的至善数各位数字之和的一半,求B的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,AC、DC为弦,∠ACD=60°,P为AB延长线上的点,∠APD=30°.
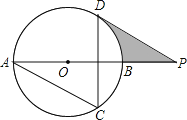
(1)求证:DP是⊙O的切线;
(2)若⊙O的半径为3cm,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】李师傅驾驶出租车匀速地从西安市送客到咸阳国际机场,全程约![]() ,设小汽车的行驶时间为
,设小汽车的行驶时间为![]() (单位:
(单位:![]() ),行驶速度为
),行驶速度为![]() (单位:
(单位:![]() ),且全程速度限定为不超过
),且全程速度限定为不超过![]() .
.
(1)求![]() 关于
关于![]() 的函数表达式;
的函数表达式;
(2)李师傅上午![]() 点驾驶小汽车从西安市出发.需在
点驾驶小汽车从西安市出发.需在![]() 分钟后将乘客送达咸阳国际机场,求小汽车行驶速度
分钟后将乘客送达咸阳国际机场,求小汽车行驶速度![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A、B是函数![]() 图象上关于原点对称的两点,且BC//x轴,AC//y轴,△ABC的面积记为S,则( )
图象上关于原点对称的两点,且BC//x轴,AC//y轴,△ABC的面积记为S,则( )
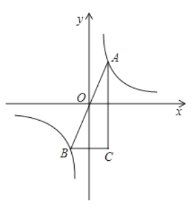
A.S=2B.S=4C.S=8D.S=1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com