
ΓΨΧβΡΩΓΩ‘ΡΕΝάμΫβΘΚ»τ‘Ύ“ΜΗωΝΫΈΜ’ΐ’ϊ ΐNΒΡΗωΈΜ ΐΉ÷”κ °ΈΜ ΐΉ÷÷°ΦδΧμ…œ ΐΉ÷6Θ§Ήι≥…“ΜΗω–¬ΒΡ»ΐΈΜ ΐΘ§Έ“Ο«≥Τ’βΗω»ΐΈΜ ΐΈΣNΒΡΓΑ÷Ν…Τ ΐΓ±Θ§»γ34ΒΡΓΑ÷Ν…Τ ΐΈΣ364Γ±ΘΜ»τΫΪ“ΜΗωΝΫΈΜ’ΐ’ϊ ΐMΦ”6ΚσΒΟΒΫ“ΜΗω–¬ ΐΘ§Έ“Ο«≥Τ’βΗω–¬ ΐΈΣMΒΡΓΑΟςΒ¬ ΐΓ±Θ§»γ34ΒΡΓΑΟςΒ¬ ΐΈΣ40Γ±Θ°
Θ®1Θ©30ΒΡΓΑ÷Ν…Τ ΐΓ± «ΓΓ ΓΓΘ§ΓΑΟςΒ¬ ΐΓ± «ΓΓ ΓΓΘ°
Θ®2Θ©«σ÷ΛΘΚΕ‘»Έ“β“ΜΗωΝΫΈΜ’ΐ’ϊ ΐAΘ§ΤδΓΑ÷Ν…Τ ΐΓ±”κΓΑΟςΒ¬ ΐΓ±÷°≤νΡή±Μ9’ϊ≥ΐΘΜ
Θ®3Θ©»τ“ΜΗωΝΫΈΜ’ΐ’ϊ ΐBΒΡΟςΒ¬ ΐΒΡΗςΈΜ ΐΉ÷÷°ΚΆ «BΒΡ÷Ν…Τ ΐΗςΈΜ ΐΉ÷÷°ΚΆΒΡ“ΜΑκΘ§«σBΒΡΉν¥σ÷ΒΘ°
ΓΨ¥πΑΗΓΩΘ®1Θ©360ΘΜ36ΘΜΘ®2Θ©¥πΑΗΦϊΫβΈωΘΜΘ®3Θ©84.
ΓΨΫβΈωΓΩ
Θ®1Θ©ΗυΨίΓΑ÷Ν…Τ ΐΓ±ΚΆΓΑΟςΒ¬ ΐΓ±ΒΡΕ®“εΦΤΥψΦ¥Ω…ΒΟ¥πΑΗΘΜΘ®2Θ©…ηAΒΡ °ΈΜ ΐΉ÷ΈΣaΘ§ΗωΈΜ ΐΉ÷ΈΣbΘ§Ζ÷±π–¥≥ωAΒΡΓΑ÷Ν…Τ ΐΓ±ΚΆΓΑΟςΒ¬ ΐΓ±Θ§«σ≤νΘ§Μ·ΦρΘ§±μ Ψ≥ω9ΒΡ±Ε ΐΘ§Φ¥Ω…÷ΛΟςΘΜΘ®3Θ©…ηBΒΡ °ΈΜ ΐΉ÷ΈΣaΘ§ΗωΈΜ ΐΉ÷ΈΣbΘ§Ζ÷±π–¥≥ωBΒΡΓΑ÷Ν…Τ ΐΓ±ΚΆΓΑΟςΒ¬ ΐΓ±ΒΡΗςΗω ΐΈΜ…œΒΡ ΐΉ÷÷°ΚΆΘ§ΓΑΟςΒ¬ ΐΓ±ΒΡΗωΈΜΩ…Ρή¥φ‘ΎΫχΈΜΘ§Ι Ζ÷ΝΫάύΦΤΥψΦ¥Ω….
ΫβΘΚΘ®1Θ©‘Ύ3ΚΆ0÷°ΦδΧμ…œ ΐΉ÷6,
Γύ30ΒΡΓΑ÷Ν…Τ ΐ «360ΘΜΓΑΟςΒ¬ ΐΓΑ «30+6=36
Ι ¥πΑΗΈΣΘΚ360ΘΜ36Θ°
Θ®2Θ©÷ΛΟςΘΚ…ηAΒΡ °ΈΜ ΐΉ÷ΈΣaΘ§ΗωΈΜ ΐΉ÷ΈΣb
‘ρΤδΓΑ÷Ν…Τ ΐ”κΓΑΟςΒ¬ ΐΓΑΖ÷±πΈΣΘΚ
100a+60+bΘΜ10a+b+6
ΥϋΟ«ΒΡ≤νΈΣΘΚ
100a+60+b-Θ®10a+b+6Θ©
=90a+54
=9Θ®10a+6Θ©
ΓύΤδΓΑ÷Ν…Τ ΐ”κΓΑΟςΒ¬ ΐΓΑ÷°≤νΡή±Μ9’ϊ≥ΐΘ°
Θ®3Θ©…ηBΒΡ °ΈΜ ΐΉ÷ΈΣaΘ§ΗωΈΜ ΐΉ÷ΈΣb
‘ρBΒΡ÷Ν…Τ ΐΒΡΗςΈΜ ΐΉ÷÷°ΚΆ «a+6+b
BΒΡΟςΒ¬ ΐΗςΈΜ ΐΉ÷÷°ΚΆ «a+b+6Θ®Β±0ΓήbΘΦ4 ±Θ©Μρa+1+Θ®6+b-10Θ©Θ®Β±4ΓήbΓή9 ±Θ©
”…Χβ“βΒΟΘΚ0ΓήbΘΦ4 ±Θ§a+b+6=![]() Θ®a+6+bΘ©
Θ®a+6+bΘ©
Γύa+b=-6Θ§≤ΜΖϊΚœΧβ“βΘΜ
Β±4ΓήbΓή9 ±Θ§a+1+Θ®6+b-10Θ©=![]() Θ®a+6+bΘ©
Θ®a+6+bΘ©
Γύa+b=12
ΓύΒ±b=4Θ§a=8 ±Θ§BΉν¥σΘ§Ήν¥σ÷ΒΈΣ84Θ°


 ≥ω≤ Ά§≤Ϋ¥σ ‘ΨμœΒΝ–¥πΑΗ
≥ω≤ Ά§≤Ϋ¥σ ‘ΨμœΒΝ–¥πΑΗ
| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΡ≥”Έ”Ψ≥Ί”–900ΝΔΖΫΟΉΥ°Θ§ΟΩ¥ΈΜΜΥ°«ΑΚσΥ°ΒΡΧεΜΐ±Θ≥÷≤Μ±δΘ°…ηΖ≈Υ°ΒΡΤΫΨυΥΌΕ»ΈΣvΝΔΖΫΟΉ/–Γ ±Θ§ΫΪ≥ΊΡΎΒΡΥ°Ζ≈Άξ–ηt–Γ ±Θ§
Θ®1Θ©«σvΙΊ”ΎtΒΡΚ· ΐ±μ¥ο ΫΘ§≤Δ–¥≥ωΉ‘±δΝΩtΒΡ»Γ÷ΒΖΕΈßΘΜ
Θ®2Θ©»τ“Σ«σ‘Ύ2.5–Γ ±÷Ν3–Γ ±ΡΎΘ®Αϋά®2.5–Γ ±”κ3–Γ ±Θ©Α―”Έ”Ψ≥ΊΡΎΒΡΥ°Ζ≈ΆξΘ§«σΖ≈Υ°ΥΌΕ»ΒΡΖΕΈßΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
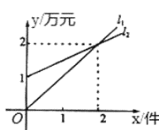
ΓΨΧβΡΩΓΩ»γΆΦΘ§![]() ±μ ΨΡ≥Μζ¥≤ΙΪΥΨ“ΜΧλΒΡœζ έ ’»κ”κΜζ¥≤œζ έΝΩΒΡΙΊœΒΘ§
±μ ΨΡ≥Μζ¥≤ΙΪΥΨ“ΜΧλΒΡœζ έ ’»κ”κΜζ¥≤œζ έΝΩΒΡΙΊœΒΘ§![]() ±μ ΨΗΟΙΪΥΨ“ΜΧλΒΡœζ έ≥…±Ψ”κΜζ¥≤œζ έΝΩΒΡΙΊœΒ.”–“‘œ¬ΥΡΗωΫα¬έΘΚΔΌ
±μ ΨΗΟΙΪΥΨ“ΜΧλΒΡœζ έ≥…±Ψ”κΜζ¥≤œζ έΝΩΒΡΙΊœΒ.”–“‘œ¬ΥΡΗωΫα¬έΘΚΔΌ![]() Ε‘”ΠΒΡΚ· ΐ±μ¥ο Ϋ «y=xΘΜΔΎ
Ε‘”ΠΒΡΚ· ΐ±μ¥ο Ϋ «y=xΘΜΔΎ![]() Ε‘”ΠΒΡΚ· ΐ±μ¥ο Ϋ «y=x+1ΘΜΔέΒ±œζ έΝΩΈΣ2Φΰ ±Θ§œζ έ ’»κΒ»”Ύœζ έ≥…±ΨΘΜΔήάϊ»σ”κœζ έΝΩ÷°ΦδΒΡΚ· ΐ±μ¥ο Ϋ «w=0.5x-1.Τδ÷–’ΐ»ΖΒΡΫα¬έΈΣ____Θ®«κΑ―Υυ”–’ΐ»ΖΒΡ–ρΚ≈Χν–¥‘ΎΚαœΏ…œΘ©.
Ε‘”ΠΒΡΚ· ΐ±μ¥ο Ϋ «y=x+1ΘΜΔέΒ±œζ έΝΩΈΣ2Φΰ ±Θ§œζ έ ’»κΒ»”Ύœζ έ≥…±ΨΘΜΔήάϊ»σ”κœζ έΝΩ÷°ΦδΒΡΚ· ΐ±μ¥ο Ϋ «w=0.5x-1.Τδ÷–’ΐ»ΖΒΡΫα¬έΈΣ____Θ®«κΑ―Υυ”–’ΐ»ΖΒΡ–ρΚ≈Χν–¥‘ΎΚαœΏ…œΘ©.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΡ≥–ΘΈΣ±μ’Ο‘ΎΓΑ¥¥ΈΡΟς≥«Θ§Βψ‘όΧ©≥«Γ± ιΜ≠±»»ϋ÷–±μœ÷”≈–ψΒΡΆ§―ßΘ§ΨωΕ®ΙΚ¬ρΥ°≤ Κ–ΜρΗ÷± ΉςΈΣΫ±ΤΖΓΘ“―÷Σ1ΗωΥ°≤ Κ–28‘ΣΓΔ1÷ßΗ÷± 30‘ΣΓΘ
Θ®1Θ©«ΓΖξΓΑ °“ΜΓ±…ΧΒξΨΌ––ΓΑ”≈Μί¥ΌœζΓ±ΜνΕ·Θ§ΨΏΧεΑλΖ®»γœ¬ΘΚΥ°≤ Κ–ΓΑΨ≈’έΓ±”≈ΜίΘΜΗ÷± 10÷ß“‘…œ≥§≥ω≤ΩΖ÷ΓΑΑΥ’έΓ±”≈ΜίΓΘ»τ¬ρ![]() ΗωΥ°≤ Κ––η“Σ
ΗωΥ°≤ Κ––η“Σ![]() ‘ΣΘ§¬ρ
‘ΣΘ§¬ρ![]() ÷ßΗ÷± –η“Σ
÷ßΗ÷± –η“Σ![]() ‘ΣΘ§«σ
‘ΣΘ§«σ![]() Θ§
Θ§![]() ΙΊ”Ύ
ΙΊ”Ύ![]() ΒΡΚ· ΐΙΊœΒ Ϋ.
ΒΡΚ· ΐΙΊœΒ Ϋ.
Θ®2Θ©Β±ΙΚ¬ρ ΐΝΩΈΣΕύ…Ό ±Θ§ΙΚ¬ρΝΫ÷÷Ϋ±ΤΖΒΡΖ―”ΟœύΆ§ΘΩ
Θ®3Θ©Β±ΙΚ¬ρ ΐΝΩΈΣ80 ±Θ§ΙΚ¬ρΝΫ÷÷Ϋ±ΤΖΒΡΖ―”Ο≤νΨύ «Εύ…ΌΘΩ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ‘ΡΕΝάμΫβΘΚ»τ ![]() ΈΣ ΐ÷α…œ»ΐΒψΘ§»τΒψ
ΈΣ ΐ÷α…œ»ΐΒψΘ§»τΒψ![]() ΒΫ
ΒΫ![]() ΒΡΨύάκ «Βψ
ΒΡΨύάκ «Βψ![]() ΒΫ
ΒΫ![]() ΒΡΨύάκ
ΒΡΨύάκ![]() ±ΕΘ§Έ“Ο«ΨΆ≥ΤΒψ
±ΕΘ§Έ“Ο«ΨΆ≥ΤΒψ![]() «
«![]() ΒΡ«…Βψ.»τ
ΒΡ«…Βψ.»τ ![]() ΈΣ ΐ÷α…œ»ΐΒψΘ§»τΒψ
ΈΣ ΐ÷α…œ»ΐΒψΘ§»τΒψ![]() ΒΫ
ΒΫ![]() ΒΡΨύάκ «Βψ
ΒΡΨύάκ «Βψ![]() ΒΫ
ΒΫ ![]() ΒΡΨύάκ“ΜΑκΘ§Έ“Ο«ΨΆ≥ΤΒψ
ΒΡΨύάκ“ΜΑκΘ§Έ“Ο«ΨΆ≥ΤΒψ![]() «
«![]() ΒΡΟνΒψ.»γΆΦΘ§Βψ
ΒΡΟνΒψ.»γΆΦΘ§Βψ![]() ±μ ΨΒΡ ΐΈΣ
±μ ΨΒΡ ΐΈΣ![]() Θ§Βψ
Θ§Βψ![]() ±μ ΨΒΡ ΐΈΣ
±μ ΨΒΡ ΐΈΣ![]() Θ§±μ Ψ
Θ§±μ Ψ![]() ΒΡΒψ
ΒΡΒψ![]() ΒΫΒψ
ΒΫΒψ![]() ΒΡΨύάκ «
ΒΡΨύάκ «![]() Θ§ΒΫΒψ
Θ§ΒΫΒψ![]() ΒΡΨύάκ «
ΒΡΨύάκ «![]() Θ§Ρ«Ο¥Βψ
Θ§Ρ«Ο¥Βψ![]() «
«![]() ΒΡ«…ΒψΘ§Βψ
ΒΡ«…ΒψΘ§Βψ![]() «
«![]() ΒΡΟνΒψ.
ΒΡΟνΒψ.
![]()
÷Σ Ε‘Υ”ΟΘΚ
(1)»γΆΦ 1Θ§Βψ![]() ±μ ΨΒΡ ΐ «
±μ ΨΒΡ ΐ «![]() Θ§Βψ
Θ§Βψ![]() ±μ ΨΒΡ ΐ «
±μ ΨΒΡ ΐ «![]() Θ§Βψ
Θ§Βψ![]() ±μ ΨΒΡ ΐ «
±μ ΨΒΡ ΐ «![]() Θ§Ρ«Ο¥Βψ
Θ§Ρ«Ο¥Βψ![]() «Θ®
«Θ®![]() ΒΡ( )
ΒΡ( )
![]()
A.«…Βψ B. ΟνΒψ C. ΈόΖ®»ΖΕ®
(2)»γΆΦ 2Θ§![]() ΈΣ ΐ÷α…œΝΫΒψΘ§Βψ
ΈΣ ΐ÷α…œΝΫΒψΘ§Βψ![]() Υυ±μ ΨΒΡ ΐΈΣ
Υυ±μ ΨΒΡ ΐΈΣ![]() Θ§Βψ
Θ§Βψ![]() Υυ±μ ΨΒΡ ΐΈΣ
Υυ±μ ΨΒΡ ΐΈΣ![]() Θ§‘ρΘ®
Θ§‘ρΘ®![]() ΒΡ«…Βψ±μ ΨΒΡ ΐ « ΘΜ
ΒΡ«…Βψ±μ ΨΒΡ ΐ « ΘΜ
![]()

ΆΊ’ΙΧα…ΐ
(3)»γΆΦ 3Θ§![]() ΈΣ ΐ÷α…œΝΫΒψΘ§Βψ
ΈΣ ΐ÷α…œΝΫΒψΘ§Βψ![]() Υυ±μ ΨΒΡ ΐΈΣ
Υυ±μ ΨΒΡ ΐΈΣ![]() Θ§Βψ
Θ§Βψ![]() Υυ±μ ΨΒΡ ΐΈΣ
Υυ±μ ΨΒΡ ΐΈΣ![]() .œ÷”–“Μ÷ΜΒγΉ”¬λ“œP¥”Βψ
.œ÷”–“Μ÷ΜΒγΉ”¬λ“œP¥”Βψ ![]() ≥ωΖΔΘ§“‘ΟΩ
≥ωΖΔΘ§“‘ΟΩ![]() ΟκΒΞΈΜΒΡΥΌΕ»œρ”“‘ΥΕ·Θ§ΒΫ¥οΒψ
ΟκΒΞΈΜΒΡΥΌΕ»œρ”“‘ΥΕ·Θ§ΒΫ¥οΒψ![]() ΆΘ÷Ι. Β±Ψ≠ΙΐΦΗΟκ ±Θ§
ΆΘ÷Ι. Β±Ψ≠ΙΐΦΗΟκ ±Θ§![]() ΚΆ
ΚΆ ![]() Τδ”–“ΜΗωΒψΈΣΤδ”ύΝΫΒψΒΡ«…Βψ? («κ÷±Ϋ”–¥≥ωΫαΙϊ)
Τδ”–“ΜΗωΒψΈΣΤδ”ύΝΫΒψΒΡ«…Βψ? («κ÷±Ϋ”–¥≥ωΫαΙϊ)
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§Βψ![]() ΕΦ‘Ύ ΐ÷α…œΘ§
ΕΦ‘Ύ ΐ÷α…œΘ§![]() ΈΣ‘≠Βψ.
ΈΣ‘≠Βψ.
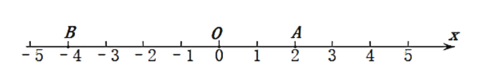
Θ®1Θ©œΏΕΈ![]() ÷–Βψ±μ ΨΒΡ ΐ « ΘΜ
÷–Βψ±μ ΨΒΡ ΐ « ΘΜ
Θ®2Θ©»τΒψ![]() “‘ΟΩΟκ
“‘ΟΩΟκ![]() ΗωΒΞΈΜ≥ΛΕ»ΒΡΥΌΕ»―Ί ΐ÷αœρ”“‘ΥΕ·ΝΥ
ΗωΒΞΈΜ≥ΛΕ»ΒΡΥΌΕ»―Ί ΐ÷αœρ”“‘ΥΕ·ΝΥ![]() ΟκΘ§Β±Βψ
ΟκΘ§Β±Βψ![]() ‘ΎΒψ
‘ΎΒψ![]() Ήσ±Ώ ±Θ§
Ήσ±Ώ ±Θ§![]() Θ§Β±Βψ
Θ§Β±Βψ![]() ÷ΝΒψ
÷ΝΒψ![]() ”“±Ώ ±Θ§
”“±Ώ ±Θ§![]() ΘΜ
ΘΜ
Θ®3Θ©»τΒψ![]() Ζ÷±π“‘ΟΩΟκ
Ζ÷±π“‘ΟΩΟκ![]() ΗωΒΞΈΜ≥ΛΕ»ΓΔ
ΗωΒΞΈΜ≥ΛΕ»ΓΔ![]() ΗωΒΞΈΜ≥ΛΕ»ΒΡΥΌΕ»―Ί ΐ÷αœρ”“‘ΥΕ·Θ§ΕχΒψ
ΗωΒΞΈΜ≥ΛΕ»ΒΡΥΌΕ»―Ί ΐ÷αœρ”“‘ΥΕ·Θ§ΕχΒψ![]() ≤ΜΕ·Θ§
≤ΜΕ·Θ§![]() ΟκΚσΘ§
ΟκΚσΘ§![]() »ΐΗωΒψ÷–”–“ΜΗωΒψ «ΝμΆβΝΫΗωΒψΈΣΕΥΒψΒΡœΏΕΈΒΡ÷–ΒψΘ§«σ
»ΐΗωΒψ÷–”–“ΜΗωΒψ «ΝμΆβΝΫΗωΒψΈΣΕΥΒψΒΡœΏΕΈΒΡ÷–ΒψΘ§«σ![]() ΒΡ÷Β.
ΒΡ÷Β.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΡ≥ ––ηΒς≤ιΗΟ –Ψ≈ΡξΦΕΡ–…ζΒΡΧεΡήΉ¥ΩωΘ§ΈΣ¥Υ≥ι»ΓΝΥ50ΟϊΨ≈ΡξΦΕΡ–…ζΫχ––“ΐΧεœρ…œΗω ΐ≤β ‘Θ§≤β ‘«ιΩωΜφ÷Τ≥…±μΗώ»γœ¬ΘΚ
Ηω ΐ | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
»Υ ΐ | 1 | 1 | 6 | 18 | 10 | 6 | 2 | 2 | 1 | 1 | 2 |
Θ®1Θ©«σ’β¥Έ≥ι―υ≤β ‘ ΐΨίΒΡΤΫΨυ ΐΓΔ÷Ύ ΐΚΆ÷–ΈΜ ΐΘΜ
Θ®2Θ©‘ΎΤΫΨυ ΐΓΔ÷Ύ ΐΚΆ÷–ΈΜ ΐ÷–Θ§Ρψ»œΈΣ”ΟΡΡ“ΜΗωΆ≥ΦΤΝΩΉςΈΣΗΟ –Ψ≈ΡξΦΕΡ–…ζ“ΐΧεœρ…œœνΡΩ≤β ‘ΒΡΚœΗώ±ξΉΦΗω ΐΫœΈΣΚœ ΘΩΦρ“ΣΥΒΟςάμ”…ΘΜ
Θ®3Θ©»γΙϊΗΟ –ΫώΡξ”–3ΆρΟϊΨ≈ΡξΦΕΡ–…ζΘ§ΗυΨίΘ®2Θ©÷–Ρψ»œΈΣΚœΗώΒΡ±ξΉΦΘ§ ‘ΙάΦΤΗΟ –Ψ≈ΡξΦΕΡ–…ζ“ΐΧεœρ…œœνΡΩ≤β ‘ΒΡΚœΗώ»Υ ΐ «Εύ…ΌΘΩ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΘ®8Ζ÷Θ©»γΆΦΘ§ΒψAΘ®3Θ§5Θ©ΙΊ”Ύ‘≠ΒψOΒΡΕ‘≥ΤΒψΈΣΒψCΘ§Ζ÷±πΙΐΒψAΘ§CΉςy÷αΒΡΤΫ––œΏΘ§”κΖ¥±»άΐΚ· ΐ![]() Θ®0ΘΦkΘΦ15Θ©ΒΡΆΦœσΫΜ”ΎΒψBΘ§DΘ§Ν§Ϋ”ADΘ§BCΘ§AD”κx÷αΫΜ”ΎΒψEΘ®©¹2Θ§0Θ©Θ°
Θ®0ΘΦkΘΦ15Θ©ΒΡΆΦœσΫΜ”ΎΒψBΘ§DΘ§Ν§Ϋ”ADΘ§BCΘ§AD”κx÷αΫΜ”ΎΒψEΘ®©¹2Θ§0Θ©Θ°

Θ®1Θ©«σkΒΡ÷ΒΘΜ
Θ®2Θ©÷±Ϋ”–¥≥ω“θ”Α≤ΩΖ÷ΟφΜΐ÷°ΚΆΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΦΉΓΔ““ΝΫ»ΥΗς…δΜς![]() ¥ΈΘ§ΦΉΥυ÷–ΒΡΜΖ ΐ «
¥ΈΘ§ΦΉΥυ÷–ΒΡΜΖ ΐ «![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§«“ΦΉΥυ÷–ΒΡΜΖ ΐΒΡΤΫΨυ ΐ «
Θ§«“ΦΉΥυ÷–ΒΡΜΖ ΐΒΡΤΫΨυ ΐ «![]() Θ§÷Ύ ΐ «
Θ§÷Ύ ΐ «![]() ΘΜ““Υυ÷–ΒΡΜΖ ΐΒΡΤΫΨυ ΐ «
ΘΜ““Υυ÷–ΒΡΜΖ ΐΒΡΤΫΨυ ΐ «![]() Θ§ΖΫ≤ν «4.ΗυΨί“‘…œ ΐΨίΘ§Ε‘ΦΉΘ§““…δΜς≥…Φ®ΒΡ’ΐ»Ζ≈–Εœ «Θ® Θ©
Θ§ΖΫ≤ν «4.ΗυΨί“‘…œ ΐΨίΘ§Ε‘ΦΉΘ§““…δΜς≥…Φ®ΒΡ’ΐ»Ζ≈–Εœ «Θ® Θ©
A.ΦΉ…δΜς≥…Φ®±»““Έ»Ε®B.““…δΜς≥…Φ®±»ΦΉΈ»Ε®
C.ΦΉΘ§““…δΜς≥…Φ®Έ»Ε®–‘œύΆ§D.ΦΉΓΔ““…δΜς≥…Φ®Έ»Ε®–‘ΈόΖ®±»Ϋœ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com