
【题目】如图,AB为⊙O的直径,AC、DC为弦,∠ACD=60°,P为AB延长线上的点,∠APD=30°.
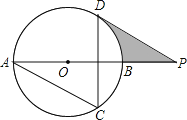
(1)求证:DP是⊙O的切线;
(2)若⊙O的半径为3cm,求图中阴影部分的面积.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】同学们参加综合实践活动时,看到木工师傅用“三弧法”在板材边角处作直角,其作法是:如图:
(1)作线段AB,分别以点A,B为圆心,AB长为半径作弧,两弧交于点C;
(2)以点C为圆心,仍以AB长为半径作弧交AC的延长线于点D;
(3)连接BD,BC.
根据以上作图过程及所作图形,下列结论中错误的是( )

A.∠ABD=90°B.CA=CB=CDC.sinA=![]() D.cosD=
D.cosD=![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)解决问题:有48支队520名运动员参加男子篮球和女子排球比赛,其中每支男子篮球队10人,每支女子排球队12人,男子篮球、女子排球队各多少支参赛?
(2)问题拓展:若有a支球队参加男子篮球比赛,b支球队参加女子排球比赛,其中每支男子篮球队m人,每支女子排球队n人,则参加篮球比赛和参加排球比赛的队员共有_____人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,P是BC上一点,E是AB上一点,PD平分∠APC,PE⊥PD,连接DE交AP于F,在以下判断中,不正确的是( )
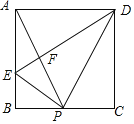
A.当P为BC中点,△APD是等边三角形
B.当△ADE∽△BPE时,P为BC中点
C.当AE=2BE时,AP⊥DE
D.当△APD是等边三角形时,BE+CD=DE
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在△ABC中,以AB为直径的⊙O交AC于点D,点E在BC上,连接BD,DE,∠CDE=∠ABD.
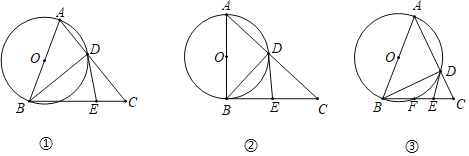
(1)求证:DE是⊙O的切线.
(2)如图②,当∠ABC=90°时,线段DE与BC有什么数量关系?请说明理由.
(3)如图③,若AB=AC=10,sin∠CDE=![]() ,求BC的长.
,求BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着社会的发展,通过微信朋友圈发布自己每天行走的步数已经成为一种时尚.“健身达人”小陈为了了解他的好友的运动情况.随机抽取了部分好友进行调查,把他们6月1日那天行走的情况分为四个类别:A(0~5000步)(说明:“0~5000”表示大于等于0,小于等于5000,下同),B(5001~10000步),C(10001~15000步),D(15000步以上),统计结果如图所示:

请依据统计结果回答下列问题:
(1)本次调查中,一共调查了 位好友.
(2)已知A类好友人数是D类好友人数的5倍.
①请补全条形图;
②扇形图中,“A”对应扇形的圆心角为 度.
③若小陈微信朋友圈共有好友150人,请根据调查数据估计大约有多少位好友6月1日这天行走的步数超过10000步?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,点
中,点![]() 在
在![]() 边上(不与点
边上(不与点![]() 重合),
重合),![]() ,垂足为点
,垂足为点![]() ,如果以
,如果以![]() 为对角线的正方形上的所有点都在
为对角线的正方形上的所有点都在![]() 的内部或边上,则称该正方形为
的内部或边上,则称该正方形为![]() 的内正方形.
的内正方形.
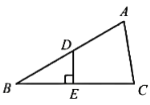
(1)如图,在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 是
是![]() 的中点,画出
的中点,画出![]() 的内正方形,直接写出此时内正方形的面积;
的内正方形,直接写出此时内正方形的面积;
(2)在平面直角坐标系![]() 中,点
中,点![]() ,
,![]() ,
,![]() .
.
①若![]() ,求
,求![]() 的内正方形的顶点
的内正方形的顶点![]() 的横坐标的取值范围;
的横坐标的取值范围;
②若对于任意的点![]() ,
,![]() 的内正方形总是存在,直接写出
的内正方形总是存在,直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:在方格纸中,每个小格的顶点叫做格点,以格点为顶点的三角形叫做格点三角形.已知图1,图2中的每一个小方格的边长都为1.
(1)![]() 的三边长为
的三边长为![]() ,
,![]() ,
,![]() .
.
①在图1中画一个符合题意的![]() ;
;
②求![]() 的边
的边![]() 上的高线长;
上的高线长;
(2)在![]() 的方格纸纸板中最多能剪下(要完整不拼凑)多少个与(1)中
的方格纸纸板中最多能剪下(要完整不拼凑)多少个与(1)中![]() 全等的三角形?并在图2中设计出来.
全等的三角形?并在图2中设计出来.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,菱形![]() 的顶点
的顶点![]() 、
、![]() 在菱形
在菱形![]() 的边上,且
的边上,且![]() ,请直接写出
,请直接写出![]() 的结果(不必写计算过程)
的结果(不必写计算过程)
(2)将图1中的菱形![]() 绕点
绕点![]() 旋转一定角度,如图2,求
旋转一定角度,如图2,求![]() ;
;
(3)把图2中的菱形都换成矩形,如图3,且![]() ,此时
,此时![]() 的结果与(2)小题的结果相比有变化吗?如果有变化,直接写出变化后的结果(不必写计算过程);若无变化,请说明理由.
的结果与(2)小题的结果相比有变化吗?如果有变化,直接写出变化后的结果(不必写计算过程);若无变化,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com