
【题目】只有1和它本身两个因数且大于1的正整数叫做素数.我国数学家陈景润哥德巴赫猜想的研究中取得了世界领先的成果.哥德巴赫猜想是“每个大于2的偶数都表示为两个素数的和”.如20=3+17.
(1)从7、11、19、23这4个素数中随机抽取一个,则抽到的数是7的概率是 ;
(2)从7、11、19、23这4个素数中随机抽取1个数,再从余下的3个数中随机抽取1个数,用画树状图或列表的方法,求抽到的两个素数之和等于30的概率.
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案科目:初中数学 来源: 题型:
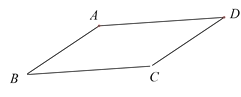
【题目】在ABCD中,∠D=30°,AB<AD.
(1)在AD边上求作一点P,使点P到边AB,BC的距离相等;(要求:尺规作图,不写作法,保留作图痕迹)
(2)在(1)的条件下,连接BP,若AB=2,求△ABP的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
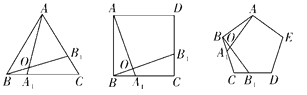
【题目】如图,下列正多边形都满足BA1=CB1,在正三角形中,我们可推得:∠AOB1=60°;在正方形中,可推得:∠AOB1=90°;在正五边形中,可推得:∠AOB1=108°,依此类推在正八边形中,AOB1=____°,在正n(n≥3)边形中,∠AOB1=____°.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,△ABC是等腰直角三角形,在两腰AB、AC外侧作两个等边三角形ABD和ACE,AM和AN分别是等边三角形ABD和ACE的角平分线,连接CM、BN,CM与AB交于点P.
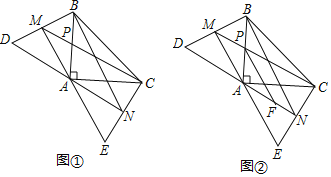
(1)求证:CM=BN;
(2)如图②,点F为角平分线AN上一点,且∠CPF=30°,求证:△APF∽△AMC;
(3)在(2)的条件下,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电视机厂要印制产品宣传材料甲印刷厂提出:每份材料收1元印制费,另需收取所有印制材料的制版费1500元;乙印刷厂提出:每份材料收2.5元印制费,不收制版费.设该电视厂在同一个印刷厂一次印的数量为![]() 份
份![]() .
.
(1)根据题意填表:
一次印制数量(份) | 300 | 500 | 1500 | … |
甲印刷厂花费(元) | 2000 | … | ||
乙印刷厂花费(元) | 1250 | … |
(2)设在甲印刷厂花费![]() 元,在乙印刷厂花费
元,在乙印刷厂花费![]() 元,分别求
元,分别求![]() ,
,![]() 关于
关于![]() 的函数解析式;
的函数解析式;
(3)根据题意填空:
①若电视厂在甲印刷厂和在乙印刷厂一次印制宣传材料的数量相同,且花费相同,则该电视厂在同一个印刷厂一次印制材料的数量为 份;
②印制800份宣传材料时,选择 印刷厂比较合算;
③电视机厂拟拿出3000元用于印制宣传材料,在 印刷厂印制宣传材料可以多一些.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)问题发现
如图1,在△OAB和△OCD中,OA=OB,OC=OD,∠AOB=∠COD=40°,连接AC,BD交于点M.填空:
①![]() 的值为 ;
的值为 ;
②∠AMB的度数为 .
(2)类比探究
如图2,在△OAB和△OCD中,∠AOB=∠COD=90°,∠OAB=∠OCD=30°,连接AC交BD的延长线于点M.请判断![]() 的值及∠AMB的度数,并说明理由;
的值及∠AMB的度数,并说明理由;
(3)拓展延伸
在(2)的条件下,将△OCD绕点O在平面内旋转,AC,BD所在直线交于点M,若OD=1,OB=![]() ,请直接写出当点C与点M重合时AC的长.
,请直接写出当点C与点M重合时AC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列内容,并解决问题.
一道习题引发的思考
小明在学习《勾股定理》一章内容时,遇到了一个习题,并对有关内容进行了研究;
习题再现:
古希腊的哲学家柏拉图曾指出,如果![]() 表示大于1的整数,
表示大于1的整数,![]() ,
,![]() ,
,![]() ,那么
,那么![]() ,
,![]() ,
,![]() 为勾股数.你认为对吗?如果对,你能利用这个结论得出一些勾股数吗?
为勾股数.你认为对吗?如果对,你能利用这个结论得出一些勾股数吗?
资料搜集:
定义:勾股数是指可以构成一个直角三角形三边的一组正整数.一般地,若三角形三边长![]() ,
,![]() ,
,![]() 都是正整数,且满足
都是正整数,且满足![]() ,那么
,那么![]() ,
,![]() ,
,![]() 称为一组勾股数.
称为一组勾股数.
关于勾股数的研究:我囯西周初数学家商高在公元前1000年发现了“勾三,股四,弦五”,这组数![]() 是世界上最早发现的一组勾股效,毕达哥拉斯学派、柏拉图学派、我国数学家刘徽、古希腊数学家丢番图都进行过勾股数的研究.习题中的表达式是柏拉图给出的勾股数公式,这个表达式未给出全部勾股数,世界上第一次给出勾股数通解公式的是《九幸算术),其勾股数公式为:
是世界上最早发现的一组勾股效,毕达哥拉斯学派、柏拉图学派、我国数学家刘徽、古希腊数学家丢番图都进行过勾股数的研究.习题中的表达式是柏拉图给出的勾股数公式,这个表达式未给出全部勾股数,世界上第一次给出勾股数通解公式的是《九幸算术),其勾股数公式为:![]() ,
,![]() ,
,![]()
![]() ,其中
,其中![]() ,
,![]() ,
,![]() 是互质的奇数.(注:
是互质的奇数.(注:![]() ,
,![]() ,
,![]() 的相同倍数组成的一组数也是勾股数)
的相同倍数组成的一组数也是勾股数)

问题解答:
(1)根据柏拉图的研究,当![]() 时,请直接写出一组勾股数;
时,请直接写出一组勾股数;
(2)若![]() 表示大于1的整数,试证明
表示大于1的整数,试证明![]() 是一组勾股数;
是一组勾股数;
(3)请举出一个反例(即写出一组勾股数),说明柏拉图给出的勾股数公式不能构造出所有的勾股数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工程队承接了60万平方米的绿化工程,由于情况有变,…设原计划每天绿化的面积为![]() 万平方米,列方程为
万平方米,列方程为![]() ,根据方程可知省路的部分是( )
,根据方程可知省路的部分是( )
A.实际每天的工作效率比原计划提高了![]() ,结果提前30天完成了这一任务
,结果提前30天完成了这一任务
B.实际每天的工作效率比原计划提高了![]() ,结果延误30天完成了这一任务
,结果延误30天完成了这一任务
C.实际每天的工作效率比原计划降低了![]() ,结果延误30天完成了这一任务
,结果延误30天完成了这一任务
D.实际每天的工作效率比原计划降低了![]() ,结果提前30天完成了这一任务
,结果提前30天完成了这一任务
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠C=90°,BC=6,DE是△ABC的中位线,点D在AB上,把点B绕点D按顺时针方向旋转α(0°<α<180°)角得到点F,连接AF,BF.下列结论:①△ABF是直角三角形;②若△ABF和△ABC全等,则α=2∠BAC或2∠ABC;③若α=90°,连接EF,则S△DEF=4.5;其中正确的结论是( )
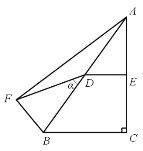
A.①②B.①③C.①②③D.②③
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com