
【题目】如图①,△ABC是等腰直角三角形,在两腰AB、AC外侧作两个等边三角形ABD和ACE,AM和AN分别是等边三角形ABD和ACE的角平分线,连接CM、BN,CM与AB交于点P.
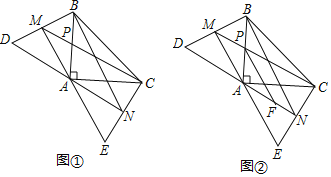
(1)求证:CM=BN;
(2)如图②,点F为角平分线AN上一点,且∠CPF=30°,求证:△APF∽△AMC;
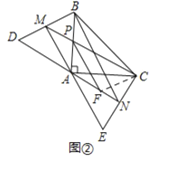
(3)在(2)的条件下,求![]() 的值.
的值.
【答案】(1)见解析(2)见解析(3)![]()
【解析】
(1)根据△ABC是等腰直角三角形,AM和AN分别是等边三角形ABD和ACE的角平分线,即可得到AB=AC,∠BAC=90°,∠BAM=∠CAN=30°,AM=AN,进而得出△BAN≌△CAM,进而得到CM=BN;
(2)依据∠APF=∠AMC,∠MAC=∠PAF=120°,即可判定△APF∽△AMC;
(3)连接CF,依据A,F,C,P四点共圆,可得∠AFP+∠CFN=90°,根据∠CFN+∠FCN=90°,可得∠FCN=∠AFP=∠ACM.再根据∠FNC=∠PAC=90°,可得△PAC∽△FNC,进而得出![]() =2①;根据△APF∽△AMC,可得
=2①;根据△APF∽△AMC,可得![]() ②,联立①②可得
②,联立①②可得![]() ,进而得到
,进而得到![]()
![]() .
.
(1)∵△ABC是等腰直角三角形,AM和AN分别是等边三角形ABD和ACE的角平分线,
∴AB=AC,∠BAC=90°,∠BAM=∠CAN=30°,AM=AN,
∴∠BAN=∠CAM=120°,
∴△BAN≌△CAM,
∴CM=BN;
(2)∵∠APF=∠APC∠CPF=∠APC30°,∠AMC=∠APC∠MAB=∠APC30°,
∴∠APF=∠AMC,
又∵∠MAC=∠PAF=120°,
∴△APF∽△AMC;
(3)如图②,连接CF,
∵△APF∽△AMC,
∴∠AFP=∠ACM,
∴A,F,C,P四点共圆,
∴∠PFC=∠PAC=90°,
∴∠AFP+∠CFN=90°,
∵∠CFN+∠FCN=90°,
∴∠FCN=∠AFP=∠ACM.
又∵∠FNC=∠PAC=90°.
∴△PAC∽△FNC,
∴![]() =
=![]() =2①;
=2①;
∵△APF∽△AMC,
∴![]() ②,
②,
由①可得,FN=![]() AP;由②可得,AF=
AP;由②可得,AF=![]() AP,
AP,
∴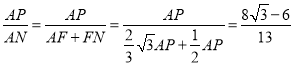 .
.
∵△APF∽△AMC,
∴![]() ,AM=AN,
,AM=AN,
∴![]()
![]() .
.


科目:初中数学 来源: 题型:
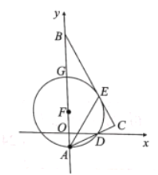
【题目】如图,在平面直角坐标系中,![]() 的斜边
的斜边![]() 在
在![]() 轴上,边
轴上,边![]() 与
与![]() 轴交于点
轴交于点![]() ,
,![]() 平分
平分![]() 交边
交边![]() 于点
于点![]() ,经过点
,经过点![]() 的圆的圆心
的圆的圆心![]() 恰好在
恰好在![]() 轴上,⊙
轴上,⊙![]() 与
与![]() 里面相交于另一点
里面相交于另一点![]() .
.
(1)求证:![]() 是⊙
是⊙![]() 的切线 ;
的切线 ;
(2)若点![]() 的坐标分别为
的坐标分别为![]() ,求⊙
,求⊙![]() 的半径及线段
的半径及线段![]() 的长;
的长;
(3)试探究线段![]() 三者之间满足的等量关系,并证明你的结论.
三者之间满足的等量关系,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】星海中学为了了解本校学生喜爱的球类运动,在本校范围内随机抽查了部分学生进行问卷调查,要求学生在“篮球、足球、排球、其它”四个选项中,选取自己最喜爱的一种球类运动(必选且只选一种).学校将收集的数据统计整理,绘制成如下两幅不完整的统计图.请你根据图中提供的信息解答下列问题:
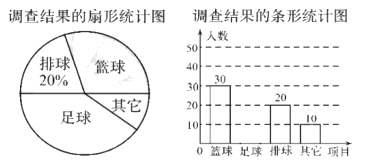
(1)在这次调查中,一共抽查了多少名学生?
(2)请通过计算补全条形统计图;
(3)如果星海中学共有1200名学生请你估计该校最喜爱足球的学生有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
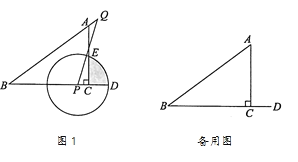
【题目】如图1,△ABC中,∠ACB=90°,AC=3,BC=4,延长BC到点D,使BD=BA,P是BC边上一点.点Q在射线BA上,PQ=BP,以点P为圆心,PD长为半径作⊙P,交AC于点E,连接PQ,设PC=x.
(1)AB= ,CD= ,当点Q在⊙P上时,求x的值;
(2)x为何值时,⊙P与AB相切?
(3)当PC=CD时,求阴影部分的面积;
(4)若⊙P与△ABC的三边有两个公共点,直接写出x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着人们“节能环保,绿色出行”意识的增强,越来越多的人喜欢骑自行车出行,也给自行车商家带来商机.某自行车行经营的A型自行车去年销售总额为8万元.今年该型自行车每辆售价预计比去年降低200元.若该型车的销售数量与去年相同,那么今年的销售总额将比去年减少10%,求:
(1)A型自行车去年每辆售价多少元?
(2)该车行今年计划新进一批A型车和新款B型车共60辆,且B型车的进货数量不超过A型车数量的两倍.已知,A型车和B型车的进货价格分别为1500元和1800元,计划B型车销售价格为2400元,应如何组织进货才能使这批自行车销售获利最多?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】只有1和它本身两个因数且大于1的正整数叫做素数.我国数学家陈景润哥德巴赫猜想的研究中取得了世界领先的成果.哥德巴赫猜想是“每个大于2的偶数都表示为两个素数的和”.如20=3+17.
(1)从7、11、19、23这4个素数中随机抽取一个,则抽到的数是7的概率是 ;
(2)从7、11、19、23这4个素数中随机抽取1个数,再从余下的3个数中随机抽取1个数,用画树状图或列表的方法,求抽到的两个素数之和等于30的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
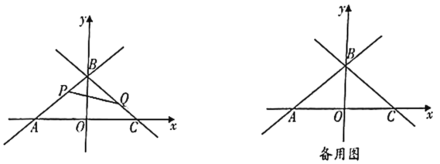
【题目】如图,在平面直角坐标系中,点![]() 为坐标原点,直线
为坐标原点,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,直线
,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,且点
,且点![]() 与点
与点![]() 关于
关于![]() 轴对称.
轴对称.
(1)求直线![]() 的解析式;
的解析式;
(2)点![]() 为线段
为线段![]() 上一点,点
上一点,点![]() 为线段
为线段![]() 上一点,
上一点,![]() ,连接
,连接![]() ,设点
,设点![]() 的横坐标为
的横坐标为![]() ,
,![]() 的面积为
的面积为![]() (
(![]() ),求
),求![]() 与
与![]() 之间的函数关系式(不要求写出自变量
之间的函数关系式(不要求写出自变量![]() 的取值范围);
的取值范围);
(3)在(2)的条件下,当![]() 取最大值时,若点
取最大值时,若点![]() 是平面内的一点,在直线
是平面内的一点,在直线![]() 上是否存在点
上是否存在点![]() ,使得以点
,使得以点![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形是菱形,若存在,请直接写出符合条件的点
为顶点的四边形是菱形,若存在,请直接写出符合条件的点![]() 坐标;若不存在,请说明理由.
坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com