
【题目】如图1,四边形![]() 内接于
内接于![]() ,
,![]() 为
为![]() 延长线上一点,
延长线上一点,![]() 平分
平分![]() .
.
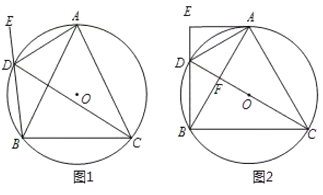
(1)求证:![]() ;
;
(2)如图2,若![]() 为直径,过
为直径,过![]() 点的圆的切线交
点的圆的切线交![]() 延长线于
延长线于![]() ,若
,若![]() ,
,![]() ,求
,求![]() 的半径.
的半径.
【答案】(1)见详解;(2)2.5
【解析】
(1)根据圆内接四边形的性质得到∠EDA=∠ACB,根据圆周角定理得到∠CDA=∠ABC,根据等腰三角形的判定定理证明;
(2)连接AO并延长交BC于H,AM⊥CD于M,根据角平分线的性质得到DM=DE=1,AE=AM=2,证明Rt△ABE≌Rt△ACM,得到CM=BE,根据勾股定理列式计算得到答案.
(1)证明:∵四边形ADBC内接于⊙O,
∴∠EDA=∠ACB,
由圆周角定理得,∠CDA=∠ABC,
∵AD平分∠EDC,
∴∠EDA=∠CDA,
∴∠ABC=∠ACB,
∴AB=AC;
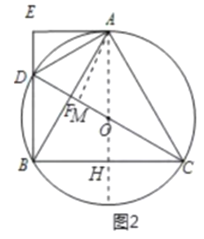
(2)解:连接AO并延长交BC于H,AM⊥CD于M,
∵AB=AC,四边形ADBC内接于⊙O,
∴AH⊥BC,又AH⊥AE,
∴AE∥BC,
∵CD为⊙O的直径,
∴∠DBC=90°,
∴∠E=∠DBC=90°,
∴四边形AEBH为矩形,
∴BH=AE=2,
∴BC=4,
∵AD平分∠EDC,∠E=90°,AM⊥CD,
∴DE=DM=1,AE=AM=2,
在Rt△ABE和Rt△ACM中,
![]()
∴Rt△ABE≌Rt△ACM(HL),
∴BE=CM,
设BE=x,CD=x+2,
在Rt△BDC中,x2+42=(x+2)2,
解得,x=3,
∴CD=5,
∴⊙O的半径为2.5.


 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,BC是⊙O的切线,D是⊙O上的一点,且AD//CO.

(1)求证:△ADB∽△OBC;
(2)若AB=2,BC=![]() ,求AD的长.(结果保留根号)
,求AD的长.(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
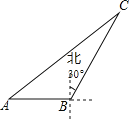
【题目】如图,海中一渔船在A处于小岛C相距70海里,若该渔船由西向东航行30海里到达B处,此时测得小岛C位于B的北偏东30°方向上,则该渔船此时与小岛C之间的距离是__海里.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,△ABC是等腰直角三角形,在两腰AB、AC外侧作两个等边三角形ABD和ACE,AM和AN分别是等边三角形ABD和ACE的角平分线,连接CM、BN,CM与AB交于点P.
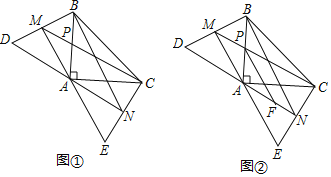
(1)求证:CM=BN;
(2)如图②,点F为角平分线AN上一点,且∠CPF=30°,求证:△APF∽△AMC;
(3)在(2)的条件下,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
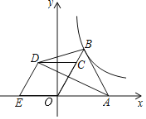
【题目】如图,在平面直角坐标系中,等边△OAB和菱形OCDE的边OA,OE都在x轴上,点C在OB边上,S△ABD=![]() ,反比例函数
,反比例函数![]() (x>0)的图象经过点B,则k的值为( )
(x>0)的图象经过点B,则k的值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)问题发现
如图1,在△OAB和△OCD中,OA=OB,OC=OD,∠AOB=∠COD=40°,连接AC,BD交于点M.填空:
①![]() 的值为 ;
的值为 ;
②∠AMB的度数为 .
(2)类比探究
如图2,在△OAB和△OCD中,∠AOB=∠COD=90°,∠OAB=∠OCD=30°,连接AC交BD的延长线于点M.请判断![]() 的值及∠AMB的度数,并说明理由;
的值及∠AMB的度数,并说明理由;
(3)拓展延伸
在(2)的条件下,将△OCD绕点O在平面内旋转,AC,BD所在直线交于点M,若OD=1,OB=![]() ,请直接写出当点C与点M重合时AC的长.
,请直接写出当点C与点M重合时AC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
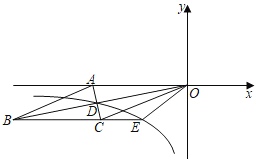
【题目】如图,菱形OABC的一边OA在x轴负半轴上.O是坐标原点,点A(﹣13,0),对角线AC与OB相交于点D,且ACOB=130,若反比例函数y=![]() (x<0)的图象经过点D,并与BC的延长线交于点E.
(x<0)的图象经过点D,并与BC的延长线交于点E.
(1)求双曲线y=![]() 的解析式;
的解析式;
(2)求S△AOB:S△OCE之值.
查看答案和解析>>
科目:初中数学 来源: 题型:
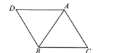
【题目】如图,已知等边![]() ,
,![]() ,将
,将![]() 绕点A顺时针旋转
绕点A顺时针旋转![]() ,得到
,得到![]() ,点E是
,点E是![]() 某边的一点,当
某边的一点,当![]() 为直角三角形时,连接
为直角三角形时,连接![]() ,作
,作![]() 于F,那么
于F,那么![]() 的长度是_________________
的长度是_________________
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com