
【题目】如图,AB是⊙O的直径,BC是⊙O的切线,D是⊙O上的一点,且AD//CO.

(1)求证:△ADB∽△OBC;
(2)若AB=2,BC=![]() ,求AD的长.(结果保留根号)
,求AD的长.(结果保留根号)
【答案】(1)详见解析;(2)![]()
【解析】
(1)根据AB为圆O的直径,根据圆周角定理得到∠D为90°,又BC为圆O的切线,根据切线性质得到∠CBO=90°,进而得到这两个角相等,又AD∥CO,根据两直线平行,得到一对同位角相等,从而利用两角对应相等的两三角形相似即可得证;
(2)根据勾股定理求得OC=![]() ,由(1)得到的相似三角形,根据相似三角形的对应边成比例得出
,由(1)得到的相似三角形,根据相似三角形的对应边成比例得出![]() ,即AD=
,即AD=![]() ,求出AD的长.
,求出AD的长.
(1)证明:∵AB是⊙O的直径,
∴∠ADB=∠90°,
∵BC是⊙O的切线,
∴∠OBC=∠90°,
∵AD∥CO,
∴∠A=∠COB,
在△ABD和△OBC中
∵∠ADB=∠OBC,∠A=∠COB,
∴△ABD∽△OCB;
(2)由(1)知,△ABD∽△OCB,
∴![]() ,即AD=
,即AD=![]() ,
,
∵AB=2,BC=![]() ,
,
∴OB=1,
∴OC=![]() =
=![]() ,
,
∴AD=![]() =
=![]() .
.


科目:初中数学 来源: 题型:
【题目】某校举办学生综合素质大赛,分“单人项目”和“双人项目”两种形式,比赛题目包括下列五类:![]() .人文艺术;
.人文艺术;![]() .历史社会;
.历史社会;![]() .自然科学;
.自然科学;![]() .天文地理;
.天文地理;![]() .体育健康.
.体育健康.
(1)若小明参加“单人项目”,他从中抽取一个题目,那么恰好抽中“自然科学”类题目的概率为_____.
(2)小林和小丽参加“双人项目”,比赛规定:同一小组的两名同学的题目类型不能相同,且每人只能抽取一次,求他们抽到“天文地理”和“体育健康”类题目的概率是多少?(用画树状图或列表的方法求解).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,O为坐标原点,△AOB是等腰直角三角形,∠AOB=90°,点A(2,1).
(1)求点B的坐标;
(2)求经过A、O、B三点的抛物线的函数表达式;
(3)在(2)所求的抛物线上,是否存在一点P,使四边形ABOP的面积最大?若存在,求出点P的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
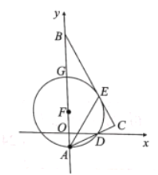
【题目】如图,在平面直角坐标系中,![]() 的斜边
的斜边![]() 在
在![]() 轴上,边
轴上,边![]() 与
与![]() 轴交于点
轴交于点![]() ,
,![]() 平分
平分![]() 交边
交边![]() 于点
于点![]() ,经过点
,经过点![]() 的圆的圆心
的圆的圆心![]() 恰好在
恰好在![]() 轴上,⊙
轴上,⊙![]() 与
与![]() 里面相交于另一点
里面相交于另一点![]() .
.
(1)求证:![]() 是⊙
是⊙![]() 的切线 ;
的切线 ;
(2)若点![]() 的坐标分别为
的坐标分别为![]() ,求⊙
,求⊙![]() 的半径及线段
的半径及线段![]() 的长;
的长;
(3)试探究线段![]() 三者之间满足的等量关系,并证明你的结论.
三者之间满足的等量关系,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD的边长为4,点E、F分别在边AB、BC上,且AE=BF=1,CE、DF交于点O.下列结论:①∠DOC=90°, ②OC=OE, ③tan∠OCD =![]() ,④
,④![]() 中,正确的有( )
中,正确的有( )
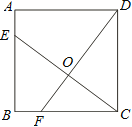
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点![]() ,
,![]() 的坐标分别为
的坐标分别为![]() 和
和![]() .
.![]() 是由
是由![]() 经过一系列变化得到的.
经过一系列变化得到的.
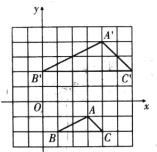
(1)请通过作图说明![]() 经过怎样的变化可以得到
经过怎样的变化可以得到![]() ;
;
(2)若![]() 为
为![]() 内任一点,则它的对应点
内任一点,则它的对应点![]() 的坐标为 .
的坐标为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com