
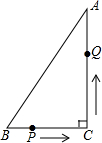
 如图,在Rt△ABC中,AC=24cm,BC=7cm,P点在BC上,从B点到C点运动(不包括C点),点P运动的速度为2cm/s;Q点在AC上从C点运动到A点(不包括A点),速度为5cm/s.若点P、Q分别从B、C同时运动,且运动时间记为t秒,请解答下面的问题,并写出探索的主要过程.
如图,在Rt△ABC中,AC=24cm,BC=7cm,P点在BC上,从B点到C点运动(不包括C点),点P运动的速度为2cm/s;Q点在AC上从C点运动到A点(不包括A点),速度为5cm/s.若点P、Q分别从B、C同时运动,且运动时间记为t秒,请解答下面的问题,并写出探索的主要过程. cm?
cm? cm,
cm, )2;
)2;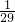 (不合题意舍去);
(不合题意舍去); =
= ×(7-2t)×5t=15
×(7-2t)×5t=15 ×PC×CQ=
×PC×CQ= ×(7-2t)×5t=
×(7-2t)×5t= ×(-2t2+7t)
×(-2t2+7t) 时,即t=
时,即t= =1.75s时,△PCQ的面积最大,
=1.75s时,△PCQ的面积最大, ×PC×CQ=
×PC×CQ= ×(7-2×1.75)×5×1.752=
×(7-2×1.75)×5×1.752=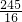 (cm2),
(cm2), ×7×24-
×7×24-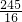 =
=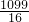 (cm2),
(cm2),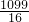 cm2.
cm2. cm2
cm2 ×PC×CQ便可求出经过2或1.5s后,S△PCQ的面积为15cm2
×PC×CQ便可求出经过2或1.5s后,S△PCQ的面积为15cm2 ×PC×CQ以及二次函数最值便可求出t=1.75s时△PCQ的面积最大,进而求出四边形BPQA的面积最小值.
×PC×CQ以及二次函数最值便可求出t=1.75s时△PCQ的面积最大,进而求出四边形BPQA的面积最小值.

科目:初中数学 来源: 题型:
 (2013•莆田质检)如图,在Rt△ABC中,∠C=90°,∠BAC的平分线AD交BC于点D,点E是AB上一点,以AE为直径的⊙O过点D,且交AC于点F.
(2013•莆田质检)如图,在Rt△ABC中,∠C=90°,∠BAC的平分线AD交BC于点D,点E是AB上一点,以AE为直径的⊙O过点D,且交AC于点F.查看答案和解析>>
科目:初中数学 来源: 题型:
 边上移动,使这个30°角的两边分别与△ABC的边AC、BC相交于点E、F,且使DE始终与AB垂直.
边上移动,使这个30°角的两边分别与△ABC的边AC、BC相交于点E、F,且使DE始终与AB垂直.查看答案和解析>>
科目:初中数学 来源: 题型:
| 5 |
 点P与点A不重合时,过点P作PQ⊥AC于点Q,以PQ为边作正方形PQMN,使点M落在线段AC上.设点P的运动时间为t(s).
点P与点A不重合时,过点P作PQ⊥AC于点Q,以PQ为边作正方形PQMN,使点M落在线段AC上.设点P的运动时间为t(s).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com