Question

已知一次函数y=ax+b（a为整数）的图象过点（17，7），它与x轴的交点为（p，0），与y轴的交点为（0，p）．若p是质数，q是正整数，那么满足条件的所有一次函数的个数为________．

Answer 1

0
分析：将（17，7），（p，0），（0，p）三点坐标代入一次函数y=ax+b中，列出方程组，根据方程组判断a、b的符号，得出p与a的关系式，根据质数的性质求a、b的值．
解答：由题意得
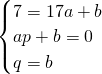
因为q是正整数，故b为正整数，a为负整数，
将第一个式子代入第二个式子得ap+7-17a=0，
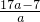
即p==17-，
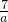
因为p是质数，故a=-1或a=-7．
当a=-1时，p=24（不是质数）；
当a=-7时，p=18（也不是质数），
故满足条件的一次函数不存在．
故答案为：0．
点评：本题考查了一次函数的综合运用．关键是根据题意列出方程组，根据整数，质数的性质，p、a的关系式得出结论．