
 建立适当的直角坐标系,表示边长为2的正六边形的各顶点的坐标.
建立适当的直角坐标系,表示边长为2的正六边形的各顶点的坐标.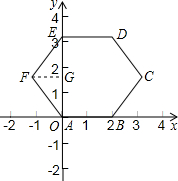 解:如图所示,以A点为原点建直角坐标系,连接AE,过F作FG⊥AE,垂足是G.
解:如图所示,以A点为原点建直角坐标系,连接AE,过F作FG⊥AE,垂足是G.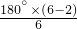 =120°(多边形内角和公式=180•(n-2),正六边形各个内角相等),
=120°(多边形内角和公式=180•(n-2),正六边形各个内角相等), =1,
=1, =
= ,
, ,
,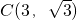 (
(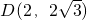 ,
,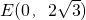 ,
,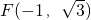 .
.

科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 实践应用:下承式混凝土连续拱圈梁组合桥,其桥面上有三对抛物线形拱圈.图(1)是其中一个拱圈的实物照片,据有关资料记载 此拱圈高AB为10.0m(含拱圈厚度和拉杆长度),横向分跨CD为40.0m.
实践应用:下承式混凝土连续拱圈梁组合桥,其桥面上有三对抛物线形拱圈.图(1)是其中一个拱圈的实物照片,据有关资料记载 此拱圈高AB为10.0m(含拱圈厚度和拉杆长度),横向分跨CD为40.0m.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com