
分析 (1)利用圆内一点和圆外一点到圆的最近距离即可得出结论;
(2)先判断出AB∥y轴,且原点到边AB的距离为2,AC∥x轴,且原点到边AC的距离为2,此时原点到边BC的距离大于2,利用圆外一点到圆上的最近距离即可确定出半径的范围;
(3)同(2)的方法,即可得出结论.
解答 解:(1)如图1,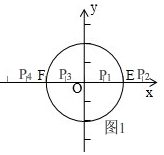 ∵⊙O的半径为2,
∵⊙O的半径为2,
∴OE=OF=2,
∵d(P,⊙O)=1,
∴PE=1或PF=1,
∴点P1(1,0),P2(3,0),P3(-1,0),P4(-3,0);
即:点P的坐标为:(-3,0),(-1,0),(1,0),(3,0),
故答案为:(-3,0),(-1,0),(1,0),(3,0);
(2)如图2,∵A(-2,-2),B(-2,6),C(6,-2),
∴AB=AC=8,∠BAC=90°,
∴∠B=∠C=90°,
∵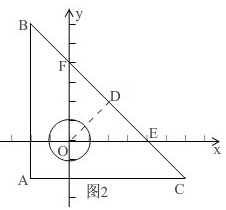 A(-2,-2),B(-2,6),
A(-2,-2),B(-2,6),
∴AB∥y轴,且原点到边AB的距离为2,
同理:AC∥x轴,原点到边AC的距离为2,
在Rt△EOF中,OE=OF=4,
∴EF=4$\sqrt{2}$,
根据三角形的面积得出OD=$\frac{OE•OF}{EF}$=2$\sqrt{2}$>2,
∵d(⊙O,△ABC)≥1,
∴0<r≤1,
(3)如图3,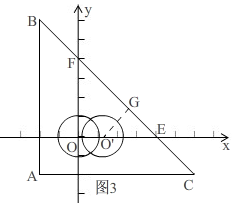 由(2)知,t>0,
由(2)知,t>0,
∵⊙D在向由移动的过程中,圆心D始终到边AC的距离为2,
圆心D到点O'时,点O'到边AB的距离是2,
过点O'作O'G⊥AB于G,
在Rt△O'EG中,∠OEF=45°,OG=2,
根据勾股定理得,O'E=2$\sqrt{2}$,
∴OO'=OE-O'E=4-2$\sqrt{2}$,
∵d(⊙D,△ABC)=1,
∴0<t≤4-2$\sqrt{2}$.
点评 此题是圆的综合题,主要考查了圆内和圆外一点到圆上的最近距离的确定方法,新定义的理解,勾股定理;解本题的关键是理解新定义的基础上,掌握圆内和圆外一点到圆上的最近距离的确定方法.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:选择题
 有一容器的形状如图所示,现匀速地向该容器内注水,直到把容器注满,在注水过程中,容器内的水面高度h与注水时间t的大致图象为( )
有一容器的形状如图所示,现匀速地向该容器内注水,直到把容器注满,在注水过程中,容器内的水面高度h与注水时间t的大致图象为( )| A. |  | B. | 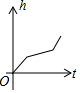 | C. | 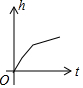 | D. | 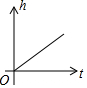 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
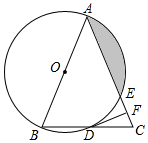 如图,在△ABC中,AB=AC,以AB为直径的⊙O分别与BC,AC交于点D,E,过点D作DF⊥AC;垂足为点F.
如图,在△ABC中,AB=AC,以AB为直径的⊙O分别与BC,AC交于点D,E,过点D作DF⊥AC;垂足为点F.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,P为矩形ABCD边上的一个动点,沿ABCD方向运动,P点运动的路程为x.△PAD的面积为y,则y与x的函数关系用图象表示大致是( )
如图,P为矩形ABCD边上的一个动点,沿ABCD方向运动,P点运动的路程为x.△PAD的面积为y,则y与x的函数关系用图象表示大致是( )| A. |  | B. |  | C. |  | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
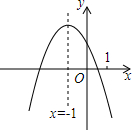 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出以下四个结论:①abc<0;②a+b+c<0;③4a+c>2b;④2a-b=0;⑤m(am+b)+b<a(m≠-1),其中,正确的结论有( )
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出以下四个结论:①abc<0;②a+b+c<0;③4a+c>2b;④2a-b=0;⑤m(am+b)+b<a(m≠-1),其中,正确的结论有( )| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
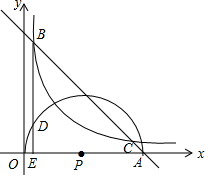 如图,已知y=-x+m(m>4)过动点A(m,0),并与反比例函数y=$\frac{4}{x}$的图象交于B、C两点(点B在点C的左边),以OA为直径作反比例函数y=$\frac{4}{x}$的图象相交的半圆,圆心为P,过点B作x轴的垂线,垂足为E,并于半圆P交于点D.
如图,已知y=-x+m(m>4)过动点A(m,0),并与反比例函数y=$\frac{4}{x}$的图象交于B、C两点(点B在点C的左边),以OA为直径作反比例函数y=$\frac{4}{x}$的图象相交的半圆,圆心为P,过点B作x轴的垂线,垂足为E,并于半圆P交于点D.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com