
����Ŀ���ס������������˿�������10������Ϸ����Ϸ�������£�
��������������Ϊ���������������6��������������6������������ƵĻ�ɫ�أ���
���������ƽ���ʱ���������Ƶ�����������ӣ�����������֮��С�ڻ����10����ʱ��������֮�;��������յ�����������������֮�ʹ���10���������յ�������0��
����Ϸ����֮ǰ˫������֪���Է�����������
���ж���Ϸ����������ǣ������յ��������һ����ʤ�������յ��������ʱ����ʤ����
�ּס��Ҿ��������������ƣ�����֮�Ͷ���5����ʱ���ϻ������ű��泯�ϵ��˿��ƣ��������ֱַ���4��5��6��7��

��1�����״����ϼ�����һ���˿��ƣ��Ҳ������ƣ����ʤ�ĸ���Ϊ ��
��2�������ȴ����ϼ�����һ���˿��ƣ������Ҵ�ʣ�µ��˿���������һ���ƣ�Ȼ��˫���������ƣ�������״ͼ������ʾ��������ƺ����п��ܵĽ�������б����ּס��ҵ������յ������������һ�ʤ�ĸ��ʣ�
���𰸡���1��![]() ����2��
����2��![]() ��
��
��������
��1��������4��5�ɻ�ʤ������6��7���һ�ʤ�����ɵõ���ʤ�ĸ��ʣ�
��2��������״ͼ�����ɵó����ۣ�
�⣺��1��������4��5�ɻ�ʤ������6��7���һ�ʤ����P����ʤ��=![]() =
=![]() ��
��
�ʴ�Ϊ��![]() ��
��
��2����ͼ��

�����п��ܵĽ���ǣ�4��5����4��6����4��7����5��4����5��6����5��7����6��4����6��5����6��7��
��7��4����7��5����7��6�� ��12�֣�
��P���һ�ʤ��=![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���׳����ҳ�ͬʱ��A�س���ȥ��B�أ���ͼ��ʾ������O��A��B��C������OC�ֱ��Ǽס��������н�������·����ʱ��Ĺ�ϵ����֪�׳���;����ͣ��36���Ӻ��ټ���ǰ��C�أ�����ͬʱ����C�أ�������˵�������ҳ����ٶ�Ϊ70ǧ��/ʱ�����׳��ٴγ�������ٶ�Ϊ100ǧ��/ʱ���������ڵ���B��ǰ�������������׳��ٴγ���ʱ���������60ǧ�ף�������ȷ���У�������
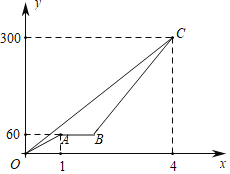
A.1��B.2��C.3��D.4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������Ϣ������Ѹ�ͷ�չ������ȥ�̳������֧����ʽ���Ӷ�������ݣ�ijУ��ѧ��ȤС�������һ�ݵ����ʾ���Ҫ��ÿ��ѡ��ֻѡһ������ϲ����֧����ʽ���ֽ�����������ͳ�Ʋ����Ƴ�����������������ͳ��ͼ������ͼ����������Ϣ����������⣺
��1����λ���������� ���ˣ�������ͳ��ͼ�У���ʾ��֧������֧��������Բ�ĽǵĶ���Ϊ�� ����
��2��������ͳ��ͼ�����������۲��ͼ��֧����ʽ���������������� ������
��3����һ�ι����У�С����С�����������������֧�������������п�������֧����ʽ��ѡһ�ַ�ʽ����֧�������û���״ͼ���б���ķ������������ǡ��ѡ��ͬһ��֧����ʽ�ĸ��ʣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���г�Ϊ![]() ����ʣ���һ������ǽ��ǽ�������ó���
����ʣ���һ������ǽ��ǽ�������ó���![]() Ϊ
Ϊ![]() ��Χ���м����һ����ʵij����λ��ԣ��軨�ԵĿ�
��Χ���м����һ����ʵij����λ��ԣ��軨�ԵĿ�![]() Ϊ
Ϊ![]() �����Ϊ
�����Ϊ![]() ��
��

��1����![]() ��
��![]() �ĺ�����ϵʽ���Ա���
�ĺ�����ϵʽ���Ա���![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��2��ҪΧ�����Ϊ![]() �Ļ��ԣ�
�Ļ��ԣ�![]() �ij��Ƕ����ף�
�ij��Ƕ����ף�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����O����ABC��һ�㣬����OB��OC������AB��OB��OC��AC���е�D��E��F��G�������ᣬ�õ��ı���DEFG��
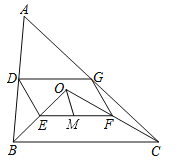
��1����֤���ı���DEFG��ƽ���ı��Σ�
��2����MΪEF���е㣬OM=3����OBC����OCB���࣬��DG�ij��ȣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��L��y��x+1��y���ڵ�A1����x����������ȡ��B1��ʹOB1��OA1������B1��A2B1��x�ᣬ��L�ڵ�A2����x����������ȡ��B2��ʹB1B2��B1A2������B2��A3B2��x�ᣬ��L�ڵ�A3����x����������ȡ��B3��ʹB2B3��B2A3�����ǡ�OA1B1���ΪS1����B1A2B2���ΪS2����B2A3B3���ΪS3������S2019����_____��
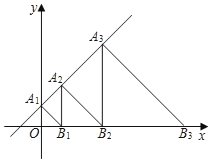
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С����ѧ��ҵ�ؼ��紴ҵ����һ����ֲ�辰�뻨�ܸ�50���ۺ�ͳ�����辰��ƽ��ÿ��������160Ԫ�����ܵ�ƽ��ÿ��������19Ԫ�����з��֣�
���辰ÿ����1�����辰��ƽ��ÿ���������2Ԫ;ÿ����1�����辰��ƽ��ÿ����������2Ԫ;�ڻ��ܵ�ƽ��ÿ������ʼ�ղ���.
С���ƻ��ڶ�����ֲ�辰�뻨�ܹ�100��������ֲ���辰�ȵ�һ������x�����ڶ����辰�뻨������������ֱ�ΪW1��W2����λ��Ԫ��
��1���ú�x�Ĵ���ʽ�ֱ��ʾW1��W2;
��2����xȡ��ֵʱ���ڶ�����ֲ���辰�뻨��������õ�������W���������������Ƕ���?
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����![]() �У�
��![]() ��
��![]() ��
��![]() ����
����![]() �ڱ�
�ڱ�![]() �ϣ�����
�ϣ�����![]() ����
����![]() ���ŵ�
���ŵ�![]() ��ת��ʹ�õ�
��ת��ʹ�õ�![]() ���
���![]() ���е�
���е�![]() �غϣ���
�غϣ���![]() �Ķ�Ӧ���ǵ�
�Ķ�Ӧ���ǵ�![]() ����
����![]() �ij�����_____��
�ij�����_____��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����Ƕ��壺����ƽ���͵��ڵ�����ƽ����2���������ν������������Σ�
���磺ij���������߳��ֱ���2��4��![]() ����Ϊ
����Ϊ![]() ��������������������������Σ�
���������������������������
��1�����ݶ��壺���ȱ������������������Ρ����������______���⣨��桱�����⡱����
��2����![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ����
����![]() ����
����![]() ��������������
��������������![]() ��
��
��3����ͼ����![]() Ϊб�߷ֱ���
Ϊб�߷ֱ���![]() ��������ֱ�������Σ���
��������ֱ�������Σ���![]() �����ı���
�����ı���![]() �ڴ��ڵ�
�ڴ��ڵ�![]() ��ʹ��
��ʹ��![]() ��
��![]() ��
��
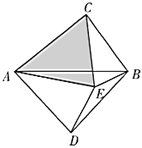
����֤��![]() �����������Σ�
������������
�ڵ�![]() ��ֱ��������ʱ����
��ֱ��������ʱ����![]() �Ķ�����
�Ķ�����
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com