
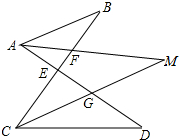
 如图,AM是∠BAD的平分线,CM是∠BCD的平分线,AM、CM交于点M,CB、AM交于点F,AD、CM交于点G,AD、CB交于点E,∠B=32°,∠D=38°.
如图,AM是∠BAD的平分线,CM是∠BCD的平分线,AM、CM交于点M,CB、AM交于点F,AD、CM交于点G,AD、CB交于点E,∠B=32°,∠D=38°.分析 (1)根据三角形内角和定理用∠B、∠M表示出∠BAM-∠BCM,再用∠B、∠M表示出∠MAD-∠MCD,再根据角平分线的定义可得∠BAM-∠BCM=∠MAD-∠MCD,然后求出∠M与∠B、∠D关系,代入数据进行计算即可得解;
(2)根据三角形内角和定理用∠B、∠M表示出∠BAM-∠BCM,再用∠B、∠M表示出∠MAD-∠MCD,再根据角平分线的定义可得∠BAM-∠BCM=∠MAD-∠MCD,然后求出∠M与∠B、∠D关系.
解答 解:(1)解:根据三角形内角和定理,∠B+∠BAM=∠M+∠BCM,
∴∠BAM-∠BCM=∠M-∠B,
同理,∠MAD-∠MCD=∠D-∠M,
∵AM、CM分别平分∠BAD和∠BCD,
∴∠BAM=∠MAD,∠BCM=∠MCD,
∴∠M-∠B=∠D-∠M,
∴∠M=$\frac{1}{2}$(∠B+∠D)=$\frac{1}{2}$(32°+38°)=35゜;
(2)证明:根据三角形内角和定理,∠B+∠BAM=∠M+∠BCM,
∴∠BAM-∠BCM=∠M-∠B,
同理,∠MAD-∠MCD=∠D-∠M,
∵AM、CM分别平分∠BAD和∠BCD,
∴∠BAM=∠MAD,∠BCM=∠MCD,
∴∠M-∠B=∠D-∠M
∴2∠M与∠B+∠D.
点评 本题考查了三角形的内角和定理,角平分线的定义.注意利用对顶角相等和三角形外角的性质求出角的关系是解题的关键,要注意整体思想的利用.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
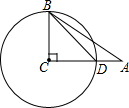 如图,在△ABC中,已知∠C=90°,sinA=$\frac{3}{5}$,以BC为半径的⊙C交AC边上一点D,若AD=4,求半径BC的长.
如图,在△ABC中,已知∠C=90°,sinA=$\frac{3}{5}$,以BC为半径的⊙C交AC边上一点D,若AD=4,求半径BC的长.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 转化 | B. | 数形结合 | C. | 演绎 | D. | 分类讨论 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图是两个互相啮合的齿轮,它们在同一时间内转动时,大齿轮和小齿轮转过的总齿数是相同的,尝试回答下面问题.
如图是两个互相啮合的齿轮,它们在同一时间内转动时,大齿轮和小齿轮转过的总齿数是相同的,尝试回答下面问题.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com