
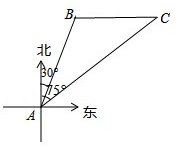
 南海是我国的南大门,如图所示,某天我国一艘海监执法船在南海海域正在进行常态化巡航,在A处测得北偏东30°方向上,距离为20海里的B处有一艘不明身份的船只正在向正东方向航行,便迅速沿北偏东75°的方向前往监视巡查,经过一段时间后,在C处成功拦截不明船只,问我海监执法船在前往监视巡查的过程中行驶了多少海里(最后结果保留整数)?
南海是我国的南大门,如图所示,某天我国一艘海监执法船在南海海域正在进行常态化巡航,在A处测得北偏东30°方向上,距离为20海里的B处有一艘不明身份的船只正在向正东方向航行,便迅速沿北偏东75°的方向前往监视巡查,经过一段时间后,在C处成功拦截不明船只,问我海监执法船在前往监视巡查的过程中行驶了多少海里(最后结果保留整数)?分析 过B作BD⊥AC,在直角三角形ABD中,利用勾股定理求出BD与AD的长,在直角三角形BCD中,求出CD的长,由AD+DC求出AC的长即可.
解答 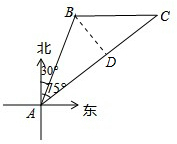 解:过B作BD⊥AC,
解:过B作BD⊥AC,
∵∠BAC=75°-30°=45°,
∴在Rt△ABD中,∠BAD=∠ABD=45°,∠ADB=90°,
由勾股定理得:BD=AD=$\frac{\sqrt{2}}{2}$×20=10$\sqrt{2}$(海里),
在Rt△BCD中,∠C=15°,∠CBD=75°,
∴tan∠CBD=$\frac{CD}{BD}$,即CD=10$\sqrt{2}$×3.732=52.77048,
则AC=AD+DC=10$\sqrt{2}$+10$\sqrt{2}$×3.732=66.91048≈67(海里),即我海监执法船在前往监视巡查的过程中行驶了67海里.
点评 此题考查了解直角三角形的应用-方向角问题,熟练掌握直角三角形的性质是解本题的关键.


科目:初中数学 来源: 题型:解答题
 如图,?ABCD中,AB=2,AD=1,∠ADC=60°,将?ABCD沿过点A的直线l折叠,使点D落到AB边上的点D′处,折痕交CD边于点E.
如图,?ABCD中,AB=2,AD=1,∠ADC=60°,将?ABCD沿过点A的直线l折叠,使点D落到AB边上的点D′处,折痕交CD边于点E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com