
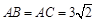 ,经过这个三角形重心的直线DE // BC,分别交边AB、AC于点D和点E,P是线段DE上的一个动点,过点P分别作PM⊥BC,PF⊥AB,PG⊥AC,垂足分别为点M、F、G.设BM = x,四边形AFPG的面积为y.
,经过这个三角形重心的直线DE // BC,分别交边AB、AC于点D和点E,P是线段DE上的一个动点,过点P分别作PM⊥BC,PF⊥AB,PG⊥AC,垂足分别为点M、F、G.设BM = x,四边形AFPG的面积为y.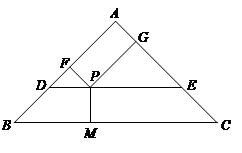
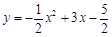 (
(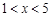 ) (3)
) (3)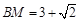 或
或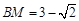 .
.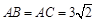 ,∴BC = 6.
,∴BC = 6.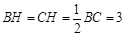 ,Q是△ABC的重心.
,Q是△ABC的重心.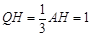 .
.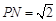 .
.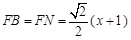 .
.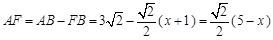 ,
,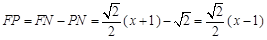 .
.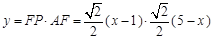 ,
,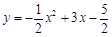 .
.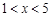 .
.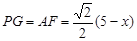 .
. .即得 PF = PG.
.即得 PF = PG.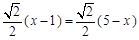 .
. .即得
.即得 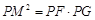 .
.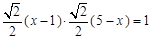 .
.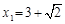 ,
,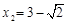 .
.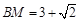 或
或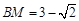 .
.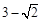 或3或
或3或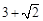 .
.

 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案科目:初中数学 来源:不详 题型:解答题
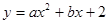 的图象与
的图象与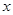 轴交于A(-3,0),B(1,0)两点,与y轴交于点C.
轴交于A(-3,0),B(1,0)两点,与y轴交于点C.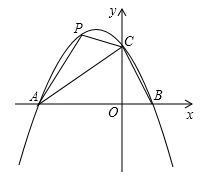
 轴,垂足为E.是否存在点Q,使以点B、Q、E为顶点的三角形与△AOC相似?若存在,直接写出点Q的坐标;若不存在,说明理由;
轴,垂足为E.是否存在点Q,使以点B、Q、E为顶点的三角形与△AOC相似?若存在,直接写出点Q的坐标;若不存在,说明理由;查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 x与BC边相交于D点.
x与BC边相交于D点.
 x经过点A,试确定此抛物线的解析式;
x经过点A,试确定此抛物线的解析式;查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 的图像过点
的图像过点 ,与
,与 轴交于点
轴交于点 .
.
 (其中
(其中 是原点);
是原点); ,使
,使 的值最小;
的值最小; 是线段
是线段 上的一个动点(不与
上的一个动点(不与 、
、 重合),过
重合),过 作
作 轴的平行线,分别交此二次函数图像及
轴的平行线,分别交此二次函数图像及 轴于
轴于 、
、 两点 . 请问
两点 . 请问 ,使
,使 . 若存在,
. 若存在, 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
| A.y1>y2>y3 | B.y1>y3>y2 | C.y3>y2>y1 | D.y3>y1>y2 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 轴上,折叠边AD,使点D落在
轴上,折叠边AD,使点D落在 轴上点F处,折痕为AE,已知AB=8,AD=10,并设点B坐标为
轴上点F处,折痕为AE,已知AB=8,AD=10,并设点B坐标为 ,其中
,其中 >0.
>0.
 的式子表示);
的式子表示);  的值;
的值;  经过图(1)中的A、E两点,如图(2),其顶点为M,连结AM,若∠OAM=90°,求
经过图(1)中的A、E两点,如图(2),其顶点为M,连结AM,若∠OAM=90°,求 、
、 、
、 的值.
的值. 查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
 x2-
x2- x与x轴交于O,A两点. 半径为1的动圆(⊙P),圆心从O点出发沿抛物线向靠近点A的方向移动;半径为2的动圆(⊙Q),圆心从A点出发沿抛物线向靠近点O的方向移动. 两圆同时出发,且移动速度相等,当运动到P,Q两点重合时同时停止运动. 设点P的横坐标为t .
x与x轴交于O,A两点. 半径为1的动圆(⊙P),圆心从O点出发沿抛物线向靠近点A的方向移动;半径为2的动圆(⊙Q),圆心从A点出发沿抛物线向靠近点O的方向移动. 两圆同时出发,且移动速度相等,当运动到P,Q两点重合时同时停止运动. 设点P的横坐标为t .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com