练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    17．在△ABC中，若AB=2，BC=1，AC=$\sqrt{3}$，则△ABC是（　　）
    A．锐角三角形B．直角三角形C．钝角三角形D．等腰三角形

    分析 欲求证是否为直角三角形，这里给出三边的长，只要验证两小边的平方和等于最长边的平方即可．

    解答 解：在△ABC中，AB=2，BC=1，AC=$\sqrt{3}$，
    ∵12+（$\sqrt{3}$）2=22，
    ∴△ABC是直角三角形．
    故选B．

    点评 本题考查勾股定理的逆定理的应用．判断三角形是否为直角三角形，已知三角形三边的长，只要利用勾股定理的逆定理加以判断即可．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

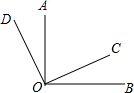    7．如图所示，∠AOB是直角，∠COD也是直角，∠AOC=65°，那么∠BOD的度数是（　　）
    A．90°+65°B．90°+2×65°C．180°-65°D．180°-2×65°

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    8．某学校九年级有6个班，每班的人数相同，从九年级的学生中任意抽取了7名学生，下列说法正确的是（　　）
    A．肯定没有同一个班级的学生
    B．可能有两名同学在一班级，但可能很小
    C．至少有三名学生在同一个班级
    D．至少有两名学生在同一个班级

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    5．无论a取何值，下列判断一定正确的是（　　）
    A．a＞a÷3B．a2＞aC．a＞-aD．a2≥0

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    12．下列运算正确的是（　　）
    A．m3•m2=m6B．（xy）8÷（xy）4=（xy）2
    C．a10÷（a7÷a2）=a5D．x4m+x2n•x2n=1（n为正整数）

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    2．如图，将四根长度相等的木条首尾相连，钉成四边形ABCD，并转动四边形ABCD使其形状改变，当∠A=60°，测得BD=1，则当∠A=90°时，BD长为（　　）
    A．1B．2C．$\sqrt{2}$D．$\sqrt{3}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    9．拓广探索
    探索“互相垂直的两直线y1=k1x+b（k1≠0）与y2=k2x+m（k2≠0）的比例系数之间的关系”
    （1）如图1，在平面直角坐标系xOy中，正方形OABC的边长为4，且OA，OC分别在x轴、y轴上，则对角线OB所在直线的解析式为y=x，对角线AC所在直线的解析式为y=-x+4．

    （2）边长为5的菱形ABCD如图2放置在网格中（网格的小正方形边长为1），且顶点都在格点上，分别求对角线BD所在直线、对角线AC所在直线的解析式；
    （3）结合（1）（2）的解答，或者改变一下菱形ABCD的位置继续探究
    ①请猜想：如果两直线y1=k1x+b（k1≠0）与y2=k2x+m（k2≠0）互相垂直，那么k1•k2=-1；
    ②请直接利用①的猜想结果解决下列问题：在平面直角坐标系中，如图3，直线y=-$\frac{1}{2}$x+5与x轴交于点B，与y轴交于点A，OC是AB边上的高，C为垂足，则点C的坐标是（2，4）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    7．如图，直线a，b与直线c，d相交，已知∠1=∠2，∠3=110°，则∠4的度数为110°．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    8．请你动手试试，过一条直线外的一点作这条直线的平行线，能作几条？由此能得出一个什么数学结论．能做一条，过直线外一点有且只有一条直线与这条直线平行．

    查看答案和解析>>

    同步练习册答案