
已知二次函数y=x2-2x-3的图象与x轴交于A、B两点(A在B的左侧),与y轴交于点C,顶点为D.
(1)求点A、B、C、D的坐标,并在下面直角坐标系中画出该二次函数的大致图象;
(2)说出抛物线y=x2-2x-3可由抛物线y=x2如何平移得到?
(3)求四边形OCDB的面积.
(1)A(﹣1,0),B(3,0),C(0,﹣3),D(1,﹣4)图形见解析;
(2)抛物线y=x2-2x-3可由y=x2先向右平移1个单位,再向下平移4个单位而得到;
(3)四边形OCDB的面积为 .
.
解析试题分析:(1)先把此二次函数化为y=(x+1)(x﹣3)的形式,即可求出A、B两点的坐标,由二次函数的解析式可知c=﹣3,故可知C点坐标,由二次函数的顶点式即可求出其顶点坐标;
(2)根据四边形OCDB的面积=S矩形OEFB﹣S△BDF﹣S△CED即可解答.
试题解析:(1)∵二次函数y=x2﹣2x﹣3可化为y=(x+1)(x﹣3),A在B的左侧,
∴A(﹣1,0),B(3,0),
∵c=﹣3,
∴C(0,﹣3),
∵x=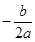 =
= =1,y=
=1,y=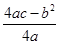 =﹣4,
=﹣4,
∴D(1,﹣4),故此函数的大致图象为: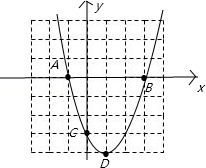
(2)抛物线y=x2-2x-3可由y=x2先向右平移1个单位,再向下平移4个单位而得到;
(3)连接CD、BD,
则四边形OCDB的面积=S矩形OEFB﹣S△BDF﹣S△CED
=OB•|OE|﹣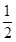 DF•|BF|﹣
DF•|BF|﹣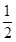 DE•CE
DE•CE
=3×4﹣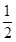 ×2×4﹣
×2×4﹣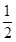 ×1×1
×1×1
=12﹣4﹣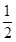
= .
. .
.
考点:二次函数图象上点的坐标特征.


科目:初中数学 来源: 题型:解答题
某职业学校三名学生到某超市参加了社会实践活动,在活动中他们参与了某种水果的销售工作,已知该水果的进价为8元/千克,下面是他们在活动结束后的对话。
A:如果以10元/千克的价格销售,那么每天可售出300千克.
B:如果以13元/千克的价格销售,那么每天可获取利润750元.
C:通过调查验证,我发现每天的销售量y(千克)与销售单价x(元)之间存在一次函数关系.
(1)求y(千克)与x(元)(x>0)的函数关系式;
(2)当销售单价为何值时,该超市销售这种水果每天获取的利润达到600元?【利润=销售量×(销售单价-进价)】
(3)一段时间后,发现这种水果每天的销售量均不低于225千克.则此时该超市销售这种水果每天获取的最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
在二次函数 中,函数y与自变量x的部分对应值如下表:
中,函数y与自变量x的部分对应值如下表:
| x | … | -1 | 0 | 1 | 2 | 3 | … |
| y | … | 8 | 3 | 0 | -1 | 0 | … |
 ?
?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图所示,在平面直角坐标系xoy中,正方形OABC的边长为2cm,点A、C分别在y轴的负半轴和x轴的正半轴上,抛物线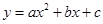 经过点A、B和D(4,
经过点A、B和D(4, ).
).
(1)求抛物线的表达式.
(2)如果点P由点A出发沿AB边以2cm/s的速度向点B运动,同时点Q由点B出发,沿BC边以1cm/s的速度向点C运动,当其中一点到达终点时,另一点也随之停止运动.设S=PQ2(cm2).
①试求出S与运动时间t之间的函数关系式,并写出t的取值范围;
②当S取 时,在抛物线上是否存在点R,使得以点P、B、Q、R为顶点的四边形是平行四边形?如果存在,求出R点的坐标;如果不存在,请说明理由.
时,在抛物线上是否存在点R,使得以点P、B、Q、R为顶点的四边形是平行四边形?如果存在,求出R点的坐标;如果不存在,请说明理由.
(3)在抛物线的对称轴上求点M,使得M到D、A的距离之差最大,求出点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
抛物线y=- 与y轴交于(0,3),
与y轴交于(0,3),
⑴求m的值;
⑵求抛物线与x轴的交点坐标及顶点坐标;
⑶当x取何值时,抛物线在x轴上方?
⑷当x取何值时,y随x的增大而增大?
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,矩形ABCD的两边长AB=18cm,AD=4cm,点P、Q分别从A、B同时出发,P在边AB上沿AB方向以每秒2cm的速度匀速运动,Q在边BC上沿BC方向以每秒1cm的速度匀速运动.设运动时间为x秒,△PBQ的面积为y(cm2).

(1)求y关于x的函数关系式,并在右图中画出函数的图像;
(2)求△PBQ面积的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
东方商场购进一批单价为20元的日用品,销售一段时间后,经调查发现,若按每件24元的价格销售时,每月能卖36件;若按每件29元的价格销售时,每月能卖21件,假定每月销售件数y(件)与价格x(元/件)之间满足关系一次函数.
(1)试求y与x的函数关系式;
(2)为了使每月获得利润为144元,问商品应定为每件多少元?
(3)为了获得了最大的利润,商品应定为每件多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
已知:如图①,在Rt△ACB中,∠C=90º,AC=6cm,BC=8cm,点P由B出发沿BC方向向点C匀速运动,速度为2cm/s;点Q由A出发沿AB方向向点B匀速运动,速度为1cm/s;连接PQ.若设运动的时间为t(s)(0<t<4),解答下列问题:
(1)当t为何值时,PQ的垂直平分线经过点B?
(2)如图②,连接CQ.设△PQC的面积为y(cm2),求y与t之间的函数关系式;
(3)如图②,是否存在某一时刻t,使线段C Q恰好把四边形ACPQ的面积分成1:2的两部分?若存在,求出此时t的值;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,矩形ABCD中,AB=16cm,AD=4cm,点P、Q分别从A、B同时出发,点P在边AB上沿AB方向以2cm/s的速度匀速运动,点Q在边BC上沿BC方向以1cm/s的速度匀速运动,当其中一点到达终点时,另一点也随之停止运动.设运动时间为x秒,△PBQ的面积为y(cm2).
(1)求y关于x的函数关系式,并写出x的取值范围;
(2)求△PBQ的面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com