
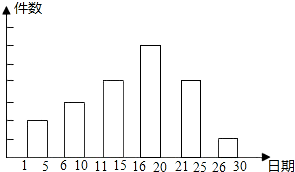
 学校举办一项小制作评比活动.作品上交时限为3月1日至30日,组委会把同学们交来的作品按时间顺序每5天组成一组,对每一组的作品件数进行统计,绘制成如图所示的统计图.已知从左到右各矩形的高度比为2:3:4:6:4:1.第三组的件数是12.
学校举办一项小制作评比活动.作品上交时限为3月1日至30日,组委会把同学们交来的作品按时间顺序每5天组成一组,对每一组的作品件数进行统计,绘制成如图所示的统计图.已知从左到右各矩形的高度比为2:3:4:6:4:1.第三组的件数是12.| 4 |
| 2+3+4+6+4+1 |
| 1 |
| 5 |
| 6 |
| 2+3+4+6+4+1 |
| 1 |
| 2+3+4+6+4+1 |
| 10 |
| 18 |
| 5 |
| 9 |
| 2 |
| 3 |
| 5 |
| 9 |
| 2 |
| 3 |
 ,
,| 2 |
| 12 |
| 1 |
| 6 |


科目:初中数学 来源: 题型:
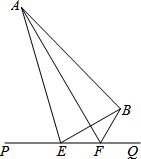 如图,大海中有A和B两个岛屿,为测量它们之间的距离,在海岸线PQ上点E处测得∠AEP=74°,∠BEQ=30°;在点F处测得∠AFP=60°,∠BFQ=60°,EF=1km.
如图,大海中有A和B两个岛屿,为测量它们之间的距离,在海岸线PQ上点E处测得∠AEP=74°,∠BEQ=30°;在点F处测得∠AFP=60°,∠BFQ=60°,EF=1km.| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com