
����Ŀ��ij��˾������A�ֲ�Ʒ��ÿ���ɱ���2Ԫ��ÿ���ۼ���3Ԫ��һ�����������10�����Ϊ�˻�ø��������˾���ó�һ���ʽ�������森���ݾ��飬ÿ��Ͷ��Ĺ���Ϊx����Ԫ��ʱ����Ʒ������������ԭ����y������y��x�Ķ��κ�������˾����Ԥ�⣬֪x��y֮��Ķ�Ӧ��ϵ�����
![]()
��1�����ݱ��У���y����x�ĺ�����ϵʽ��
��2������������������ܶ��ȥ�ɱ����ѣ�����д��������S����Ԫ�������x����Ԫ���ĺ�����ϵʽ��
��3����������ĺ�����ϵʽ������Ϊÿ��Ͷ����ٹ�������ʣ�Ϊʲô��
���𰸡���1��y=��![]() x2+
x2+![]() x+1����2��S=��x2+5x+10��3��ÿ��Ͷ�����Ϊ2.5��Ԫ����ʣ���Ϊ��ʱ�ɻ��������
x+1����2��S=��x2+5x+10��3��ÿ��Ͷ�����Ϊ2.5��Ԫ����ʣ���Ϊ��ʱ�ɻ��������
��������
�����������1������������ϵʽΪy=ax2+bx+c���ɱ��������ô���ϵ��������ý���ʽ��
��2�����ݣ�������=ÿ��������������������к�����ϵʽ���ɣ�
��3������2���к�����ϵʽ�䷽�ɶ���ʽ����֪����������ʱͶ��Ĺ���x��
�⣺��1������������ϵʽΪy=ax2+bx+c��
�ѣ�0��1������1��1.5������2��1.8���ֱ������ʽ��
�ã�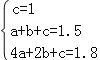 ��
��
��ã�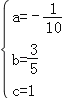 ��
��
��y=��![]() x2+
x2+![]() x+1��
x+1��
��2���������⣬�У�S=��3��2����10y��x
=����![]() x2+
x2+![]() x+1����10��x
x+1����10��x
=��x2+5x+10��
��3����S=��x2+5x+10=����x��![]() ��2+
��2+![]() ��
��
��ÿ��Ͷ�����Ϊ2.5��Ԫ����ʣ���Ϊ��ʱ�ɻ��������



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ�����������ҷ�����˶����涨�����˶�4m������4m����ô�����˶�4m������ ��
A. ��4m B. 4m C. 8m D. ��8m
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ,��ƽ��ֱ������ϵ��,��A,B������ֱ�Ϊ��-1��0������3��0��,��ͬʱ����A,B�ֱ�����ƽ��2����λ,������ƽ��1����λ,�ֱ�õ���A,B�Ķ�Ӧ��C,D,����AC,BD.(1)���C,D�����꼰�ı���ABCD�����S��ABDC;(2)��y�����Ƿ����һ��P,����PA,PB,ʹS��ABC=S��ABDC,����������һ��,�����P������;��������,��˵������;(3)��P���߶�BD�ϵ�һ������,����PC,PO,����P��BD���ƶ�ʱ(����B,D�غ�)�������н���:(1) ![]() ��ֵ����,(2)
��ֵ����,(2) ![]() ��ֵ����,��������ֻ��һ������ȷ��,�����ҳ�������۲�����ֵ.
��ֵ����,��������ֻ��һ������ȷ��,�����ҳ�������۲�����ֵ.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪A��B�������30 km��С����6 km/h���ٶȴ�A���е�B�صľ���Ϊykm�����е�ʱ��Ϊxh����y��x֮��ĺ�������ʽ����ָ��y��x��ʲô������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ABCD ������A�á�B�á�C�á�D ��ֵ������( )
A. 2��5��2��5 B. 3��4��4��5 C. 4��4��3��2 D. 2��3��5��6
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵxoy�У�����ABCD�ı�AB��x���ϣ���AB=3��BC=2��ֱ��y=x��2������C����y���ڵ�G��

��1����C��D������ֱ���C�� ����D�� ����
��2������ֱ��y=x��2���Ҿ�����C��D�������ߵĽ���ʽ��
��3������2���е������߶�����ֱ��y=x��2ƽ�ƣ�ƽ�ƺ�������߽�y���ڵ�F������Ϊ��E�������EF=EGʱ�����ߵĽ���ʽ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com