
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:初中数学 来源: 题型:


查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:


|
|
|
查看答案和解析>>
科目:初中数学 来源:2012年江苏省中考模拟数学试卷 题型:解答题
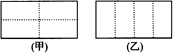
20.(9分)现有一张长和宽之比为2:1的长方形纸片.将它折两次(第一次折后也可以打开铺平再折第二次).使得折痕将纸片分为面积相等且不重叠的四个部分(称为一个操作),如图甲(虚线表示折痕).

除图甲外,请你再给出三个不同的操作,分别将折痕画在图①至图③中(规定:一个操作得到的四个图形,和另一个操作得到的四个图形,如果能够“配对”得到四组全等的图形,那么就认为是相同的操作.如图乙和图甲是相同的操作).

|
|
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com