
已知双曲线 与直线
与直线 相交于A、B两点.第一象限上的点M(m,n)(在A点左侧)是双曲线
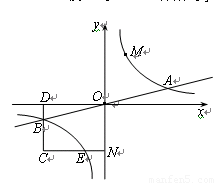
相交于A、B两点.第一象限上的点M(m,n)(在A点左侧)是双曲线 上的动点.过点B作BD∥y轴交x轴于点D.过N(0,﹣n)作NC∥x轴交双曲线
上的动点.过点B作BD∥y轴交x轴于点D.过N(0,﹣n)作NC∥x轴交双曲线 于点E,交BD于点C.
于点E,交BD于点C.
(1)若点D坐标是(﹣8,0),求A、B两点坐标及k的值.
(2)若B是CD的中点,四边形OBCE的面积为4,求直线CM的解析式.
(1)16 (2)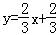
解析试题分析:(1)根据B点的横坐标为﹣8,代入 中,得y=﹣2,得出B点的坐标,即可得出A点的坐标,再根据k=xy求出即可;
中,得y=﹣2,得出B点的坐标,即可得出A点的坐标,再根据k=xy求出即可;
(2)根据S矩形DCNO=2mn=2k,S△DBO=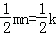 ,S△OEN=
,S△OEN=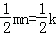 ,即可得出k的值,进而得出B,C点的坐标,再求出解析式即可.
,即可得出k的值,进而得出B,C点的坐标,再求出解析式即可.
解:(1)∵D(﹣8,0),
∴B点的横坐标为﹣8,代入 中,得y=﹣2.
中,得y=﹣2.
∴B点坐标为(﹣8,﹣2).
∵A、B两点关于原点对称,∴A(8,2).
∴k=xy=8×2=16;
(2)∵N(0,﹣n),B是CD的中点,A、B、M、E四点均在双曲线上,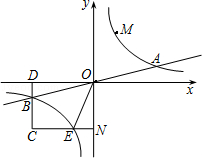
∴mn=k,B(﹣2m,﹣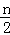 ),C(﹣2m,﹣n),E(﹣m,﹣n).
),C(﹣2m,﹣n),E(﹣m,﹣n).
S矩形DCNO=2mn=2k,S△DBO=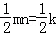 ,S△OEN=
,S△OEN=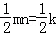 ,
,
∴S四边形OBCE=S矩形DCNO﹣S△DBO﹣S△OEN=k=4.
∴k=4.
∵B(﹣2m,﹣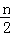 )在双曲线
)在双曲线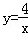 与直线
与直线 上
上
∴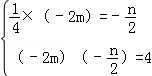 得
得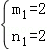
 (舍去)
(舍去)
∴C(﹣4,﹣2),M(2,2).
设直线CM的解析式是y=ax+b,把C(﹣4,﹣2)和M(2,2)代入得:
解得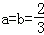 .
.
∴直线CM的解析式是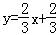 .
.
考点:反比例函数与一次函数的交点问题.
点评:此题主要考查了待定系数法函数解析式以及一次函数与反比例函数交点的性质,根据四边形OBCE的面积为4得出k的值是解决问题的关键.


科目:初中数学 来源:2012届江苏泰兴市黄桥初级中学八年级下期中数学试卷(带解析) 题型:解答题
已知双曲线 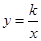 与直线
与直线 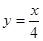 相交于A、B两点.第一象限上的点M(m,n)(在A点左侧)是双曲线
相交于A、B两点.第一象限上的点M(m,n)(在A点左侧)是双曲线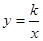 上的动点.过点B作BD∥y轴交x轴于点D.过N(0,-n)作NC∥x轴交双曲线
上的动点.过点B作BD∥y轴交x轴于点D.过N(0,-n)作NC∥x轴交双曲线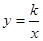 于点E,交BD于点C.
于点E,交BD于点C.
【小题1】若点D坐标是(-8,0),求A、B两点坐标及k的值.
【小题2】若B是CD的中点,四边形OBCE的面积为4,求直线CM的解析式.
【小题3】在(2)的条件下,若P为x轴上一点,是否存在△OMP为等腰三角形?若存在,写出P点坐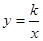 标;若不存在,说明理由。
标;若不存在,说明理由。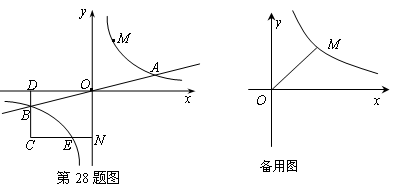
查看答案和解析>>
科目:初中数学 来源:2008年初中毕业升学考试(江苏南通卷)数学(带解析) 题型:解答题
已知双曲线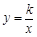 与直线
与直线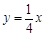 相交于A、B两点.第一象限上的点M(m,n)(在A点左侧)是双曲线
相交于A、B两点.第一象限上的点M(m,n)(在A点左侧)是双曲线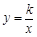 上的动点.过点B作BD∥y轴交x轴于点D.过N(0,-n)作NC∥x轴交双曲线
上的动点.过点B作BD∥y轴交x轴于点D.过N(0,-n)作NC∥x轴交双曲线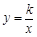 于点E,交BD于点C.
于点E,交BD于点C.
(1)若点D坐标是(-8,0),求A、B两点坐标及k的值.
(2)若B是CD的中点,四边形OBCE的面积为4,求直线CM的解析式.
(3)设直线AM、BM分别与y轴相交于P、Q两点,且MA=pMP,MB=qMQ,求p-q的值.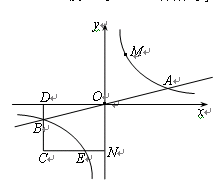
查看答案和解析>>
科目:初中数学 来源:2008年初中毕业升学考试(江苏南通卷)数学(解析版) 题型:解答题
已知双曲线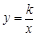 与直线
与直线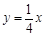 相交于A、B两点.第一象限上的点M(m,n)(在A点左侧)是双曲线
相交于A、B两点.第一象限上的点M(m,n)(在A点左侧)是双曲线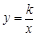 上的动点.过点B作BD∥y轴交x轴于点D.过N(0,-n)作NC∥x轴交双曲线
上的动点.过点B作BD∥y轴交x轴于点D.过N(0,-n)作NC∥x轴交双曲线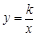 于点E,交BD于点C.
于点E,交BD于点C.
(1)若点D坐标是(-8,0),求A、B两点坐标及k的值.
(2)若B是CD的中点,四边形OBCE的面积为4,求直线CM的解析式.
(3)设直线AM、BM分别与y轴相交于P、Q两点,且MA=pMP,MB=qMQ,求p-q的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com