
【题目】如图,△ABC中,AC=BC=10cm,AB=12cm,点D是AB的中点,连结CD,动点P从点A出发,沿A→C→B的路径运动,到达点B时运动停止,速度为每秒2cm,设运动时间为t秒. 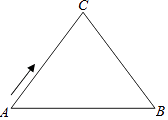
(1)求CD的长;
(2)当t为何值时,△ADP是直角三角形?
(3)直接写出:当t为何值时,△ADP是等腰三角形?
【答案】
(1)解:如图所示,AC=BC=10cm,AB=12cm,点D是AB的中点,
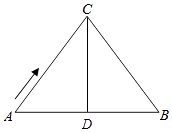
∴CD⊥AB,AD=DB= ![]() AB=6cm,
AB=6cm,
∴Rt△ACD中,CD= ![]() =8cm
=8cm
(2)解:分两种情况:
①如图所示,当DP⊥AC时,△ADP是直角三角形,
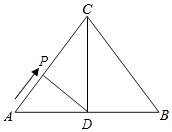
∵∠A=∠A,∠APD=∠ADC=90°,
∴△APD∽△ADC,
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,
,
解得t=1.8,
②如图所示,当PD⊥AD时,△ADP是直角三角形,

此时点P与点C重合,AP=AC=10,
∴t= ![]() =5,
=5,
综上所述,当t=1.8或5秒时,△ADP是直角三角形
(3)解:分三种情况:
①如图所示,当PA=PD时,过点P作PE⊥AD于E,则AE= ![]() AD=3,
AD=3,
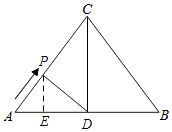
∵PE∥CD,
∴△APE∽△ACD,
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,
,
解得t= ![]() ;
;
②如图所示,当AP=AD时,2t=6,
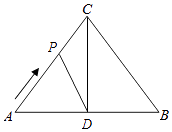
∴t= ![]() =3;
=3;
③如图所示,当AD=PD时,过点D作DF⊥AP于F,则AF= ![]() AP=t,
AP=t,
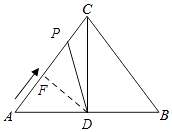
∵∠A=∠A,∠AFD=∠ADC=90°,
∴△AFD∽△ADC,
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,
,
解得t=3.6,
综上所述,当t=2.5或3或3.6秒时,△ADP是等腰三角形
【解析】(1)根据AC=BC=10cm,AB=12cm,点D是AB的中点,运用等腰三角形的性质,求得AD的长,再根据勾股定理求得CD即可;(2)分两种情况进行讨论:当DP⊥AC时,△ADP是直角三角形,当PD⊥AD时,△ADP是直角三角形,分别根据相似三角形的性质进行求解即可;(3)分三种情况进行讨论:当PA=PD时,当AP=AD时,当AD=PD时,分别作辅助线构造相似三角形,运用相似三角形的对应边成比例,求得t的值即可.
【考点精析】本题主要考查了等腰三角形的性质和勾股定理的概念的相关知识点,需要掌握等腰三角形的两个底角相等(简称:等边对等角);直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】老师对甲、乙两人的五次数学测验成绩进行统计,得出两人五次测验成绩的平均分均为90分,方差分别是S甲2=51、S乙2=12.则成绩比较稳定的是(填“甲”、“乙”中的一个).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“五一”期间,某校若干名教师带领学生组成旅游团到A地旅游,甲旅行社的收费标准是:教师无优惠,学生按原价七折优惠;乙旅行社的收费标准是:5人以上(含5人)可购团体票,团体票按原价的八折优惠.这两家旅行社的全票价均为每人300元.
(1)已知,如果这个旅行团选择甲旅行社则花费3300元:如果选择乙旅行社则花费比选择甲旅行社多60元,请问这个旅行团教师有多少人?学生有多少人?
(2)如果教师人数不变,则学生人数在什么范围内时,选择乙旅行社更省钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①所示,四边形ABCD是长方形,将长方形ABCD折叠,点B恰好落在AD边上的点E处,折痕为FG,如图②所示: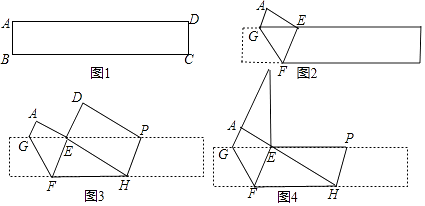
(1)图②中,证明:GE=EF;
(2)将图②折叠,点C与点E重合,折痕为PH,如图③所示,当∠FEH=90°时:
①当EF=5,EH=12时,求长方形ABCD的面积;
②将图③中的△PED绕着点E旋转,使点D与点A重合,点P与点M重合,
如图④,求证:△GEM≌△FEH.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】王大爷存入银行2500元,定期一年到期后扣除20%的利息税后得到本息和为2650元,若这种储蓄的年利率为x , 那么可得方程( )
A.2500(1+x)=2650
B.2500(1+x%)=2650
C.2500(1+x80%)=2650
D.2500(1+x20%)=2650
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的口袋里装有四个小球,球面上分别标有数字﹣2、0、1、2,它们除数字不同外没有任何区别,每次实验先搅拌均匀.
(1)从中任取一球,求抽取的数字为负数的概率;
(2)从中任取一球,将球上的数字记为x(不放回);再任取一球,将球上的数字记为y,试用画树状图(或列表法)表示所有可能出现的结果,并求“x+y>0”的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com