Question

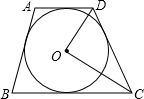
4．如图所示，在⊙O的外切梯形ABCD中，若AD∥BC，则∠DOC的大小是（　　）

• A． 45°
• B． 60°
• C． 70°
• D． 90°

Answer 1

分析 先由平行线的性质得同旁内角互补：∠ADC+∠BCD=180°，由切线长定理得：OD平分∠ADC，OC平分∠BCD，所以∠ODC+∠OCD=90°，根据三角形的内角和得：∠DOC=90°．

解答 解：∵AD∥BC，
∴∠ADC+∠BCD=180°，
∵梯形ABCD内切于圆O，
∴OD平分∠ADC，OC平分∠BCD，
∴∠ODC=$\frac{1}{2}$∠ADC，∠OCD=$\frac{1}{2}$∠BCD，
∴∠ODC+∠OCD=$\frac{1}{2}$∠ADC+$\frac{1}{2}$∠BCD=$\frac{1}{2}$×180°=90°，
∴∠DOC=90°，
故选D．

点评 本题考查了梯形的内切圆和平行线的性质，熟知圆外一点引圆的两条切线，这点与圆心的连线平分切线所成的夹角；此题是常考题型，两对角平分线构成直角三角形，要熟练掌握．