
 如图所示,在平面直角坐标系中,⊙C经过坐标原点O,且与x轴,y轴分别相交于M(4,0),N(0,3)两点.已知抛物线开口向上,与⊙C交于N,H,P三点,P为抛物线的顶点,抛物线的对称轴经过点C且垂直x轴于点D.
如图所示,在平面直角坐标系中,⊙C经过坐标原点O,且与x轴,y轴分别相交于M(4,0),N(0,3)两点.已知抛物线开口向上,与⊙C交于N,H,P三点,P为抛物线的顶点,抛物线的对称轴经过点C且垂直x轴于点D.分析 (1)连接OC,由勾股定理可求得MN的长,则可求得OC的长,由垂径定理可求得OD的长,在Rt△OCD中,可求得CD的长,则可求得PD的长,可求得P点坐标;
(2)可设抛物线的解析式为顶点式,再把N点坐标代入可求得抛物线解析式;
(3)由抛物线解析式可求得A、B的坐标,由S四边形OPMN=8S△QAB可求得点Q到x轴的距离,且点Q只能在x轴的下方,则可求得Q点的坐标,再证明△QAB∽△OBN即可.
解答 解:
(1)如图,连接OC,
∵M(4,0),N(0,3),
∴OM=4,ON=3,
∴MN=5,
∴OC=$\frac{1}{2}$MN=$\frac{5}{2}$,
∵CD为抛物线对称轴,
∴OD=MD=2,
在Rt△OCD中,由勾股定理可得CD=$\sqrt{O{C}^{2}-O{D}^{2}}$=$\sqrt{(\frac{5}{2})^{2}-{2}^{2}}$=$\frac{3}{2}$,
∴PD=PC-CD=$\frac{5}{2}$-$\frac{3}{2}$=1,
∴P(2,-1);
(2)∵抛物线的顶点为P(2,-1),
∴设抛物线的函数表达式为y=a(x-2)2-1,
∵抛物线过N(0,3),
∴3=a(0-2)2-1,解得a=1,
∴抛物线的函数表达式为y=(x-2)2-1,即y=x2-4x+3;
(3)在y=x2-4x+3中,令y=0可得0=x2-4x+3,解得x=1或x=3,
∴A(1,0),B(3,0),
∴AB=3-1=2,
∵ON=3,OM=4,PD=1,
∴S四边形OPMN=S△OMP+S△OMN=$\frac{1}{2}$OM•PD+$\frac{1}{2}$OM•ON=$\frac{1}{2}$×4×1+$\frac{1}{2}$×4×3=8=8S△QAB,
∴S△QAB=1,
设Q点纵坐标为y,则$\frac{1}{2}$×2×|y|=1,解得y=1或y=-1,
当y=1时,则△QAB为钝角三角形,而△OBN为直角三角形,不合题意,舍去,
当y=-1时,可知P点即为所求的Q点,
∵D为AB的中点,
∴AD=BD=QD,
∴△QAB为等腰直角三角形,
∵ON=OB=3,
∴△OBN为等腰直角三角形,
∴△QAB∽△OBN,
综上可知存在满足条件的点Q,其坐标为(2,-1).
点评 本题为二次函数的综合应用,涉及勾股定理、垂径定理、待定系数法、相似三角形的性质和判定、二次函数的性质等知识.在(1)中利用垂径定理得到OD=2,从而求得CD的长是解题的关键,在(2)中注意设抛物线的顶点式更容易求解,在(3)中求得Q点的纵坐标是解题的关键.本题考查知识点较多,综合性较强,难度适中.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 4.64×105 | B. | 4.64×106 | C. | 4.64×107 | D. | 4.64×108 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
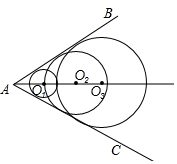 如图,∠BAC=60°,点O从A点出发,以2cm/s的速度沿∠BAC的角平分线向右运动,在运动过程中,以O为圆心的圆始终保持与∠BAC的两边相切,设⊙O的面积为S(cm2),则⊙O的面积S与圆心O运动的时间t(s)的函数图象大致为( )
如图,∠BAC=60°,点O从A点出发,以2cm/s的速度沿∠BAC的角平分线向右运动,在运动过程中,以O为圆心的圆始终保持与∠BAC的两边相切,设⊙O的面积为S(cm2),则⊙O的面积S与圆心O运动的时间t(s)的函数图象大致为( )| A. | 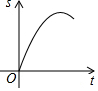 | B. | 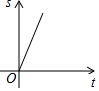 | C. |  | D. | 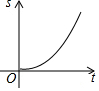 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 册数 | 0 | 1 | 2 | 3 | 4 |
| 人数 | 4 | 12 | 16 | 17 | 1 |
| A. | 中位数是2 | B. | 众数是17 | C. | 平均数是2 | D. | 方差是2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y=x2+2x+1 | B. | y=x2+2x-1 | C. | y=x2-2x+1 | D. | y=x2-2x-1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
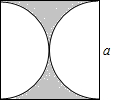 如图所示,边长为a的正方形中阴影部分的面积为( )
如图所示,边长为a的正方形中阴影部分的面积为( )| A. | a2-π($\frac{a}{2}$)2 | B. | a2-πa2 | C. | a2-πa | D. | a2-2πa |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com