
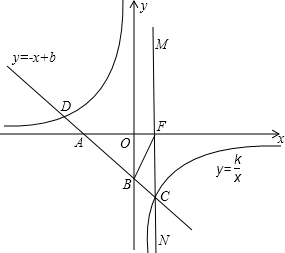
 直线y=-x+b与双曲线y=
直线y=-x+b与双曲线y= 相交于点D(-4,1)、C(1,m),并分别与坐标轴交于A、B两点,过点C作直线MN⊥x轴于F点,连接BF.
相交于点D(-4,1)、C(1,m),并分别与坐标轴交于A、B两点,过点C作直线MN⊥x轴于F点,连接BF. 相交于点D(-4,1),
相交于点D(-4,1), ,解得k=-4,
,解得k=-4, ;
;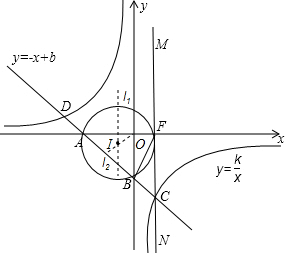 ∵直线解析式为y=-x-3;双曲线解析式为y=-
∵直线解析式为y=-x-3;双曲线解析式为y=- ,
,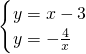 ,解得
,解得 或
或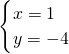 ,
,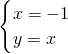 ,解得
,解得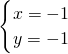 ,
,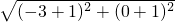 =
= ,
,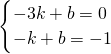 ,解得
,解得 ,
, x-
x-
 ×1-
×1- =-
=- ≠-2,
≠-2, 即可得出结论;
即可得出结论;

 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案科目:初中数学 来源: 题型:
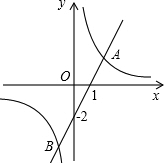 已知直线y=2x-2与双曲线图y=
已知直线y=2x-2与双曲线图y=| k | x |
查看答案和解析>>
科目:初中数学 来源: 题型:
 点,且P(-1,0),C(
点,且P(-1,0),C(| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
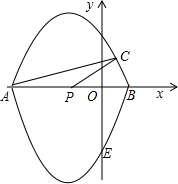
 如图,在平面直角坐标系xOy中,经过点A,C,B的抛物线的一部分与经过点A,E,B的抛物线的一部分组合成一条封闭曲线,我们把这条封闭曲线称为“双抛物线”.已知P为AB中点,且P(-1,0),C(
如图,在平面直角坐标系xOy中,经过点A,C,B的抛物线的一部分与经过点A,E,B的抛物线的一部分组合成一条封闭曲线,我们把这条封闭曲线称为“双抛物线”.已知P为AB中点,且P(-1,0),C( -1,1),E(0,-3),S△CPA=1.
-1,1),E(0,-3),S△CPA=1.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 点,且P(-1,0),C(
点,且P(-1,0),C( -1,1),E(0,-3),S△CPA=1.
-1,1),E(0,-3),S△CPA=1.查看答案和解析>>
科目:初中数学 来源:2009-2010学年新人教版九年级(上)期末数学复习试卷(解析版) 题型:解答题
 -1,1),E(0,-3),S△CPA=1.
-1,1),E(0,-3),S△CPA=1.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com