
 (1)作△ABC的外角∠BCD,再作∠BCD的平分线CE(用尺规作图,保留作图痕迹,不写作法);
(1)作△ABC的外角∠BCD,再作∠BCD的平分线CE(用尺规作图,保留作图痕迹,不写作法);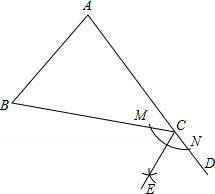 解:(1)如图所示:
解:(1)如图所示: ∠BCD,
∠BCD, ∠BCD,
∠BCD, MN长为半径画弧,两弧交于一点E,画射线CE即可;
MN长为半径画弧,两弧交于一点E,画射线CE即可; ∠BCD,再根据三角形内角与外角的关系可得∠B+∠A=∠BCD,再由∠B=∠A,可得∠A=
∠BCD,再根据三角形内角与外角的关系可得∠B+∠A=∠BCD,再由∠B=∠A,可得∠A= ∠BCD,进而得到∠A=∠ECD,根据同位角相等两直线平行可证明AB∥CE.
∠BCD,进而得到∠A=∠ECD,根据同位角相等两直线平行可证明AB∥CE.

科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,已知A是直线l外的一点,B是l上的一点.
如图,已知A是直线l外的一点,B是l上的一点.查看答案和解析>>
科目:初中数学 来源:2012届浙江省临海市灵江中学九年级2月月考数学卷 题型:解答题
某课题小组对课本的习题进行了如下探索,请逐步思考并解答:
【小题1】
 (1)(人教版教材习题24.4的第2题)如图1,两个大小一样的传送轮连接着一条传送带,两个传动轮中心的距离是10m,求这条传送带的长_________.
(1)(人教版教材习题24.4的第2题)如图1,两个大小一样的传送轮连接着一条传送带,两个传动轮中心的距离是10m,求这条传送带的长_________.
【小题2】(2)改变图形的数量;
如图2、将传动轮增加到3个,每个传动轮的直径是3m,每两个传动轮中心的距离是10m, 求这条传送带的长__________.
【小题3】( 3)改变动态关系,将静态问题升华为动态问题:
3)改变动态关系,将静态问题升华为动态问题:
如图3,一个半径为1cm的⊙P沿边长为2πcm的等边三角形△ABC的外沿作无滑动滚动一周,求圆心P经过的路径长?⊙P自转了多少周?
【小题4】(4) 拓展与应用
如图4,一个半径为1cm的⊙P沿半径为3cm的⊙O外沿作无滑动滚动一周,则⊙P自转了多少周?
查看答案和解析>>
科目:初中数学 来源:2012年浙教版初中数学七年级下 1.6作三角形练习卷(解析版) 题型:填空题
根据下列要求,判断是否一定能作出图形:
①过已知三点作一条直线;
②作直线OP的垂直平分线MN;
③过点A作线段MN的垂线AB;
④过点A作线段MN的垂直平分线;
⑤过已知线段外一点作其平行线;
⑥作△ABC的边BC的高AD且平分BC;
⑦以O为圆心作弧;
⑧以O为圆心任意长为半径作弧.
能作出图形的是_________,不能作出图形的是__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com