
【题目】如图,已知抛物线P:y=ax2+bx+c(a≠0)与x轴交于A、B两点(点A在x轴的正半轴上),与y轴交于点C,矩形DEFG的一条边DE在线段AB上,顶点F、G分别在线段BC、AC上,抛物线P上部分点的横坐标对应的纵坐标如下:
x | … | ﹣3 | ﹣2 | 1 | 2 | … |
y | … |
| ﹣4 |
| 0 | … |
(1)求A、B、C三点的坐标;
(2)若点D的坐标为(m,0),矩形DEFG的面积为S,求S与m的函数关系,并指出m的取值范围;
(3)当矩形DEFG的面积S取最大值时,连接DF并延长至点M,使FM=kDF,若点M不在抛物线P上,求k的取值范围.
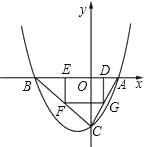
【答案】(1)A(2,0),B(﹣4,0),C(0,﹣4);(2)SDEFG=12m﹣6m2(0<m<2);(3)k≠![]() 且k>0.
且k>0.
【解析】
试题分析:(1)根据图表可以得到,抛物线经过的四点的坐标,根据待定系数法,设y=ax2+bx+c,把其中三点的坐标代入,就可以求得函数解析式.进而可以求出A、B、C的坐标;(2)表示出矩形的长和宽是解决问题的关键,先证△ADG∽△AOC,AD=2﹣m,根据相似三角形的对应边的比相等,就可以用m表示出DG的长,再根据△BEF∽△BOC,就可以表示出BE,进而得到OE,于是ED就可以表示出来.因而S与m的函数关系就可以得到;(3)当矩形DEFG的面积S取最大值时,就是函数的值是最大值时,根据二次函数的性质就可以求出相应的m的值.则矩形的四个顶点的坐标就可以求出,根据待定系数法就可以求出直线DF的解析式.可以求出直线DF与抛物线的交点的坐标,根据FM=kDF,就可以表示出M的坐标,把M的坐标代入函数就可以得到一个关于k的方程,求出k的值,判断是否满足函数的解析式即可.
试题解析:(1)根据待定系数法,设y=ax2+bx+c(a≠0),任取x,y的三组值代入,求出解析式为y=![]() x2+x﹣4,令y=0,求出x1=﹣4,x2=2;令x=0,得y=﹣4,∴A、B、C三点的坐标分别是A(2,0),B(﹣4,0),C(0,﹣4).(2)由题意,△ADG∽△AOC,所以
x2+x﹣4,令y=0,求出x1=﹣4,x2=2;令x=0,得y=﹣4,∴A、B、C三点的坐标分别是A(2,0),B(﹣4,0),C(0,﹣4).(2)由题意,△ADG∽△AOC,所以![]() ,而AO=2,OC=4,AD=2﹣m,故DG=4﹣2m,又△BEF∽△BOC,所以
,而AO=2,OC=4,AD=2﹣m,故DG=4﹣2m,又△BEF∽△BOC,所以![]() ,EF=DG,得BE=4﹣2m,∴DE=3m,∴SDEFG=DGDE=(4﹣2m)3m=12m﹣6m2(0<m<2),故S=12m﹣6m2(0<m<2);(3)如下图,连接DF并延长,∵SDEFG=12m﹣6m2(0<m<2),∴m=1时,矩形的面积最大,且最大面积是6.当矩形面积最大时,其顶点为D(1,0),G(1,﹣2),F(﹣2,﹣2),E(﹣2,0),设直线DF的解析式为y=kx+b,易知,k=
,EF=DG,得BE=4﹣2m,∴DE=3m,∴SDEFG=DGDE=(4﹣2m)3m=12m﹣6m2(0<m<2),故S=12m﹣6m2(0<m<2);(3)如下图,连接DF并延长,∵SDEFG=12m﹣6m2(0<m<2),∴m=1时,矩形的面积最大,且最大面积是6.当矩形面积最大时,其顶点为D(1,0),G(1,﹣2),F(﹣2,﹣2),E(﹣2,0),设直线DF的解析式为y=kx+b,易知,k=![]() ,b=﹣
,b=﹣![]() ,∴y=
,∴y=![]() x﹣
x﹣![]() ,又可求得抛物线P的解析式为:y=
,又可求得抛物线P的解析式为:y=![]() x2+x﹣4,令
x2+x﹣4,令![]() x﹣
x﹣![]() =
=![]() x2+x﹣4,可求出x=
x2+x﹣4,可求出x=![]() .设射线DF与抛物线P相交于点N,则N的横坐标为
.设射线DF与抛物线P相交于点N,则N的横坐标为![]() ,过N作x轴的垂线交x轴于H,有
,过N作x轴的垂线交x轴于H,有![]() =
=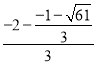 =
=![]() ,点M不在抛物线P上,即点M不与N重合时,此时k的取值范围是k≠
,点M不在抛物线P上,即点M不与N重合时,此时k的取值范围是k≠![]() 且k>0.
且k>0.


 导学全程练创优训练系列答案
导学全程练创优训练系列答案科目:初中数学 来源: 题型:
【题目】太阳与地球的平均距离大约是150 000 000千米,数据150 000 000用科学记数法表示为( )
A.1.5×108
B.1.5×109
C.0.15×109
D.15×107
查看答案和解析>>
科目:初中数学 来源: 题型:
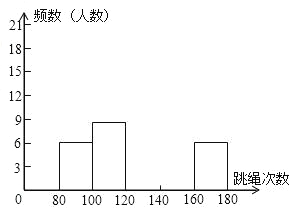
【题目】为了进一步了解八年级学生的身体素质情况,体育老师对八年级(1)班50位学生进行一分钟跳绳次数测试,以测试数据为样本,绘制出部分频数分布表和部分频数分布直方图.如下所示:
组别 | 次数x | 频数(人数) |
第1组 | 80≤x<100 | 6 |
第2组 | 100≤x<120 | 8 |
第3组 | 120≤x<140 | a |
第4组 | 140≤x<160 | 18 |
第5组 | 160≤x<180 | 6 |
请结合图表完成下列问题:
(1)表中的a= ;
(2)请把频数分布直方图补充完整;
(3)这个样本数据的中位数落在第 组;
(4)若八年级学生一分钟跳绳次数(x)达标要求是:x<120不合格;120≤x<140为合格;140≤x<160为良;x≥160为优.根据以上信息,请你给学校或八年级同学提一条合理化建议: .
查看答案和解析>>
科目:初中数学 来源: 题型:
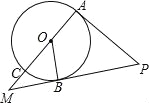
【题目】如图,AC是⊙O的直径,OB是⊙O的半径,PA切⊙O于点A,PB与AC的延长线交于点M,∠COB=∠APB.
(1)求证:PB是⊙O的切线;
(2)当OB=3,PA=6时,求MB,MC的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com