
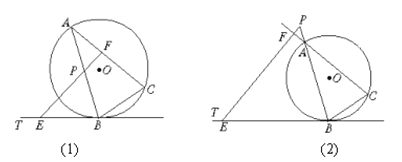
【题目】已知:△ABC是⊙O的内接三角形,BT为⊙O的切线,B为切点,P为直线AB上一点,过P作BC的平行线交直线BT于点E,交直线AC于点F.
(1)如图 (1)所示,当P在线段AB上时,求证:PA·PB=PE·PF;
(2)如图 (2)所示,当P为线段BA延长线上一点时,第(1)题的结论还成立吗?如果成立,请给出证明;如果不成立,请说明理由.
【答案】(1)证明见解析;(2)对谁成立,证明见解析
【解析】
(1)利用圆周角、弦切角间的关系证明△APF∽△BPE,根据相似三角形的性质证明 PAPB=PEPF 成立.
(2)当点P在线段BA的延长线上时,(1)的结论仍成立.先证明∠AFP=∠PBE,再由∠BPE=∠FPA,可得△PAF∽△PEB,根据成比例线段证明 PAPB=PEPF 成立.
证明:(1) 如图1,连接![]() 延长
延长![]() 与圆交于
与圆交于![]()
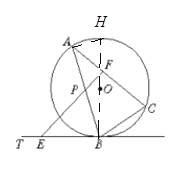
∵EB为⊙O的切线,
![]()
![]() 为⊙O的直径,
为⊙O的直径,
![]()
![]()
![]()
![]()
∴∠ACB=∠ABE,
∵EF∥BC,
∴∠AFP=∠ACB,
故∠AFP=∠ABE.
![]() ∠APF=∠EPB,
∠APF=∠EPB,
∴△APF∽△BPE,
![]()
∴PAPB=PEPF.
(2)结论成立,理由如下:
∵EB为⊙O的切线,结合(1)问:
∴∠ACB=∠ABT,
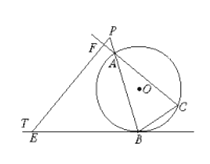
∵EF∥BC,
∴∠ACB =∠AFP,
![]()
∴∠AFP=∠PBE.
![]() ∠BPE=∠FPA,
∠BPE=∠FPA,
![]() △PAF∽△PEB,
△PAF∽△PEB,
![]()
∴PAPB=PEPF.
当点P在线段BA的延长线上时,(1)的结论仍成立.


 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案科目:初中数学 来源: 题型:
【题目】在每个小正方形的边长为1的网格中,点![]() ,
,![]() ,
,![]() 均在格点上,点
均在格点上,点![]() ,
,![]() 分别为线段
分别为线段![]() ,
,![]() 上的动点.
上的动点.
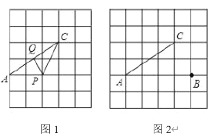
(I)如图(1),当点![]() ,
,![]() 分别为
分别为![]() ,
,![]() 中点时,
中点时,![]() 的值为__________;
的值为__________;
(Ⅱ)当![]() 取得最小值时,在如图(2)所示的网格中,用无刻度的真尺,画出线段
取得最小值时,在如图(2)所示的网格中,用无刻度的真尺,画出线段![]() ,
,![]() ,简要说明点
,简要说明点![]() 和点
和点![]() 的位置是如何找到的(不要求证明)__________.
的位置是如何找到的(不要求证明)__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某旅行团计划今年暑假组织一个老年人团去昆明旅游,预定宾馆住宿时,有住宿条件一样的甲、乙两家宾馆供选择,其收费标准为每人每天120元,并且各自推出不同的优惠方案.甲家是35人(含35人)以内的按标准收费,超过35人的,超出部分按九折收费;乙家是45人(含45人)以内的按标准收费,超过45人的,超出部分按八折收费.设老年团的人数为![]() .
.
(1)根据题意,用含有![]() 的式子填写下表:
的式子填写下表:
|
|
|
| |
甲宾馆收费/元 |
| 5280 | ||
乙宾馆收费/元 |
|
| 5400 |
(2)当老年人团的人数为何值时,在甲、乙两家宾馆的花费相同?如果老年人团的人数超过60人,在哪家宾馆住宿比较省钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
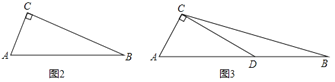
【题目】如图,平面内的两条直线l1、l2,点A、B在直线l2上,过点A、B两点分别作直线l1的垂线,垂足分别为A1、B1,我们把线段A1B1叫做线段AB在直线l2上的正投影,其长度可记作T(AB,CD)或T(AB,l2),特别地,线段AC在直线l2上的正投影就是线段A1C,请依据上述定义解决如下问题.
(1)如图1,在锐角△ABC中,AB=5,T(AC,AB)=3,则T(BC,AB)= ;
(2)如图2,在Rt△ABC中,∠ACB=90°,T(AC,AB)=4,T(BC,AB)=9,求△ABC的面积;
(3)如图3,在钝角△ABC中,∠A=60°,点D在AB边上,∠ACD=90°,T(AD,AC)=2,T(BC,AB)=6,求T(BC,CD).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在我们学习过的数学教科书中,有一个数学活动,其具体操作过程是:
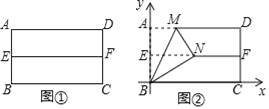
第一步:对折矩形纸片![]() ,使
,使![]() 与
与![]() 重合,得到折痕
重合,得到折痕![]() ,把纸片展开(如图①);
,把纸片展开(如图①);
第二步:再一次折叠纸片,使点![]() 落在
落在![]() 上,并使折痕经过点
上,并使折痕经过点![]() ,得到折痕
,得到折痕![]() ,同时得到线段
,同时得到线段![]() (如图②).
(如图②).
如图②所示建立平面直角坐标系,请解答以下问题:
(Ⅰ)设直线![]() 的解析式为
的解析式为![]() ,求
,求![]() 的值;
的值;
(Ⅱ)若![]() 的延长线与矩形
的延长线与矩形![]() 的边
的边![]() 交于点
交于点![]() ,设矩形的边
,设矩形的边![]() ,
,![]() ;
;
(i)若![]() ,
,![]() ,求
,求![]() 点的坐标;
点的坐标;
(ii)请直接写出![]() 、
、![]() 应该满足的条件.
应该满足的条件.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在证明定理“三角形的中位线平行于第三边,且等于第三边的一半”时,小明给出如下部分证明过程.
已知:在![]() 中,
中,![]() 分别是边
分别是边![]() 的中点.
的中点.
求证: .
证明:如图,延长![]() 到点
到点![]() ,使
,使![]() ,连接
,连接![]() ,
,
···
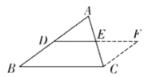
(1)补全求证:
(2)请根据添加的辅助线,写出完整的证明过程;
(3)若![]() 求边
求边![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
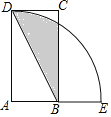
【题目】如图,四边形ABCD为矩形,以A为圆心,AD为半径的弧交AB的延长线于点E,连接BD,若AD=2AB=4,则图中阴影部分的面积为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
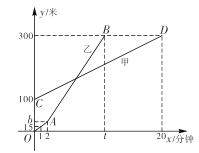
【题目】甲、乙二人都是户外运动爱好者,在一次登山活动中,甲、乙二人距出发点的高度![]() (单位:米),
(单位:米),![]() (单位:米)与乙登山时间 x (单位:分钟)之间的函数图象如图所示,根据图象所提供的信息解答下列问题:
(单位:米)与乙登山时间 x (单位:分钟)之间的函数图象如图所示,根据图象所提供的信息解答下列问题:
(1)甲登山的速度是每分钟 米,乙在 2 分钟时提速,提速时距地面的高度![]() 为______米;
为______米;
(2)若乙提速后,乙的速度是甲登山速度的 3 倍,请分别求出甲、乙二人登山全过程中,登山时距地面的高度![]() ,
, ![]() 与乙登山时间
与乙登山时间![]() 之间的函数关系式;
之间的函数关系式;
(3)在(2)的条件下,乙登山多长时间追上了甲? 此时乙距提速时的高度为多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知抛物线![]() 与
与![]() 轴相交于
轴相交于![]() 、
、![]() 两点(
两点(![]() 点在
点在![]() 点的左侧),与
点的左侧),与![]() 轴相交于
轴相交于![]() 点,且
点,且![]() .
.

(1)求这条抛物线的解析式;
(2)如图2,![]() 点在
点在![]() 轴上,且在
轴上,且在![]() 点的右侧,
点的右侧,![]() 点为抛物线上第二象限内的点,连接
点为抛物线上第二象限内的点,连接![]() 交抛物线于第二象限内的另外一点
交抛物线于第二象限内的另外一点![]() ,点
,点![]() 到
到![]() 轴的距离与点
轴的距离与点![]() 到
到![]() 轴的距离之比为
轴的距离之比为![]() ,已知
,已知![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)如图3,在(2)的条件下,点![]() 由
由![]() 出发,沿
出发,沿![]() 轴负方向运动,连接
轴负方向运动,连接![]() ,点
,点![]() 在线段
在线段![]() 上,连接
上,连接![]() ,
,![]() ,过点
,过点![]() 作
作![]() ,与抛物线相交于点
,与抛物线相交于点![]() ,若
,若![]() ,求点
,求点![]() 的坐标.
的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com